إظهار الرسائل ذات التسميات هندسة مستوية. إظهار كافة الرسائل
إظهار الرسائل ذات التسميات هندسة مستوية. إظهار كافة الرسائل
1 كيف نوجد المساحة المشتركة بين تقاطع الدائرتين في هذا المثال ؟
الاثنين، 8 أبريل 2013
التسميات:
هندسة مستوية
دائرتان طولي نصفى قطراهما 8 سم . 15 سم والبعد بين مركزيهما 17 سم اوجد مساحة المنطقة المشتركة بين الدائرتين لاقرب سم²
---------------------------------------------------------------------------------------------------------------------------------
تعتمد الفكرة على قانون مساحة القطعة الدائرية..
هـ - جاهـ
القانون هو : ـــــــــــــــــ نق²
2
أنظر الرابط : http://ar.wikipedia.org/wiki/%D9%82%D8%B7%D8%B9%D8%A9_%D8%AF%D8%A7%D8%A6%D8%B1%D9%8A%D8%A9
حيث نق هي نصف قطر الدائرة، هـ هي زاوية القطاع الدائري الحاوي للقطعة الدائرية .. وهذا ما نحن بصدده، فنحن لدينا نق لكلتا الدائرتين، ويبقى فقط إيجاد هذه الزاوية في كل قطعة، ولتكن مساحة القطة الدائرية الأولى م1 ، والثانية م1 .
مساحة تقاطع الدائرتين = م1 + م2
المهمة الآن هي إيجاد الزاوية هـ1 ، هـ2
الحل : المثلث أ هـ1 هـ2 قائم الزاوية في أ .. لماذا ؟
ببساطة طبق عكس نظرية فيثاغورث .. لديك :
نق1 = 15 ، نق2 = 8 والمسافة بينهما = 17
وبحسبة بسيطة نستنتج أن : ²17 = ²8 + ²15 إذن المثلث أ هـ1 هـ2 قائم الزاوية في أ .
لديك نظرية تقول : نصف القطر عمودي على الوتر وينصفه ..
ونظرية أخرى تقول : في المثلث المتساوي الساقين فيه العمود الساقط على القاعدة ينصف الزاوية المقابلة له.
من النظريتين السابقتين نستنتج أن قياس الزاوية هـ1 = 2× قياس(أ هـ1 هـ2)
المقابل 8
من حساب المثلثات : جا(هـ1\2) = ــــــــــــ = ــــــــــــ
الوتر 17
8 8
ومنها هـ1\2 = جا^-1(ــــــــ) اذاً : هـ1 = 2جا^-1(ــــــــــ)
17 17
بنفس الطريقة (وحتى لا نعيد نفس الفكرة) :
15
هـ2 = 2جا^-1(ـــــــــ)
17
ملحوظة : الزوايا بالتقدير الدائري .. ولذلك عند الحسابات يجب أن تقوم بضبط الآلة الحاسبة على التقدير الدائري أولاً .. (وهذه الخطوة هامة جداً)
هـ1 - جا(هـ1) 2جا^-1(8\17) - جا[2جا^-1(8\7)]
م1 = ـــــــــــــــــــــ نق²1 = ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ × ²15
2 2
≈ 16.8 سم²
هـ2 - جا(هـ2) 2جا^-1(15\17) - جا[2جا^-1(15\7)]
م1 = ـــــــــــــــــــــ نق²1 = ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ × ²8
2 2
م2 ≈ 42.6 سم²
مساحة تقاطع الدائرتين = م1+م2 ≈ 16.8 + 42.6 ≈ 59.4 سم²
تعتمد الفكرة على قانون مساحة القطعة الدائرية..
هـ - جاهـ
القانون هو : ـــــــــــــــــ نق²
2
أنظر الرابط : http://ar.wikipedia.org/wiki/%D9%82%D8%B7%D8%B9%D8%A9_%D8%AF%D8%A7%D8%A6%D8%B1%D9%8A%D8%A9
حيث نق هي نصف قطر الدائرة، هـ هي زاوية القطاع الدائري الحاوي للقطعة الدائرية .. وهذا ما نحن بصدده، فنحن لدينا نق لكلتا الدائرتين، ويبقى فقط إيجاد هذه الزاوية في كل قطعة، ولتكن مساحة القطة الدائرية الأولى م1 ، والثانية م1 .
مساحة تقاطع الدائرتين = م1 + م2
المهمة الآن هي إيجاد الزاوية هـ1 ، هـ2
الحل : المثلث أ هـ1 هـ2 قائم الزاوية في أ .. لماذا ؟
ببساطة طبق عكس نظرية فيثاغورث .. لديك :
نق1 = 15 ، نق2 = 8 والمسافة بينهما = 17
وبحسبة بسيطة نستنتج أن : ²17 = ²8 + ²15 إذن المثلث أ هـ1 هـ2 قائم الزاوية في أ .
لديك نظرية تقول : نصف القطر عمودي على الوتر وينصفه ..
ونظرية أخرى تقول : في المثلث المتساوي الساقين فيه العمود الساقط على القاعدة ينصف الزاوية المقابلة له.
من النظريتين السابقتين نستنتج أن قياس الزاوية هـ1 = 2× قياس(أ هـ1 هـ2)
المقابل 8
من حساب المثلثات : جا(هـ1\2) = ــــــــــــ = ــــــــــــ
الوتر 17
8 8
ومنها هـ1\2 = جا^-1(ــــــــ) اذاً : هـ1 = 2جا^-1(ــــــــــ)
17 17
بنفس الطريقة (وحتى لا نعيد نفس الفكرة) :
15
هـ2 = 2جا^-1(ـــــــــ)
17
ملحوظة : الزوايا بالتقدير الدائري .. ولذلك عند الحسابات يجب أن تقوم بضبط الآلة الحاسبة على التقدير الدائري أولاً .. (وهذه الخطوة هامة جداً)
هـ1 - جا(هـ1) 2جا^-1(8\17) - جا[2جا^-1(8\7)]
م1 = ـــــــــــــــــــــ نق²1 = ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ × ²15
2 2
≈ 16.8 سم²
هـ2 - جا(هـ2) 2جا^-1(15\17) - جا[2جا^-1(15\7)]
م1 = ـــــــــــــــــــــ نق²1 = ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ × ²8
2 2
م2 ≈ 42.6 سم²
مساحة تقاطع الدائرتين = م1+م2 ≈ 16.8 + 42.6 ≈ 59.4 سم²
0 كيف نثبت ان أكبر زاوية فى المثلث قطعاً هى أكبر من 60 درجة ؟
الاثنين، 29 أكتوبر 2012
التسميات:
حساب مثلثات,
هندسة مستوية
• مجموع زوايا المثلث = 180 درجة .
ليكن المثلث هو أ ب جـ ، لدينا : أ + ب + جـ = 180 ومنها : أ + جـ = 180 - ب
لتكن الزاوية ب أكبر زاوية ... هذا يؤدى بنا الى أن : ب > أ ، ب > جـ
بجمع المتباينتين معاً : 2ب > أ + جـ ولكن أ + جـ = 180 - ب .. بالتعويض
2ب > 180 - ب بجمع ب للطرفين ...
3ب > 180 بقسمة الطرفين على 3
ب > 60 وهو المطلوب إثباته .
ليكن المثلث هو أ ب جـ ، لدينا : أ + ب + جـ = 180 ومنها : أ + جـ = 180 - ب
لتكن الزاوية ب أكبر زاوية ... هذا يؤدى بنا الى أن : ب > أ ، ب > جـ
بجمع المتباينتين معاً : 2ب > أ + جـ ولكن أ + جـ = 180 - ب .. بالتعويض
2ب > 180 - ب بجمع ب للطرفين ...
3ب > 180 بقسمة الطرفين على 3
ب > 60 وهو المطلوب إثباته .
2 اوجد قياس اصغر زوايا المثلث ا ب جـ الذي فيه 15 أب = 10 ب جـ = 12 أجـ
الأربعاء، 24 أكتوبر 2012
التسميات:
حساب مثلثات,
هندسة مستوية
حقيقة : قياس أصغر زواية فى المثلث هى التى تقابل أصغر ضلع .
15 أب = 10 ب جـ = 12 أجـ
أصغر ضلع هو أ ب لماذاً ؟ لأن اصغر ضلع
هو الذى معامله يكون أكبر .. كيف ذلك ؟
اذا قُلنا أن 1 دولار = 6 جنيه (تقريباً)
هذا يعنى أن الجنيه أقل من الدولار .
الضلع أب تقابله الزواية جـ ..
اذا كان هذا الشىء يبدو ساذجاً عندك فأسعمل
قوانين النسبة والتناسب :
نفرض أن : 15 أب = 10 ب جـ = 12 أجـ = م
حيث م = ثابت التناسب .
وهذا يدلنا على اننا يمكن أن نضع التناسب
السابق لكن فى صورة أخرى .....
أ ب ب جـ أ جـ
ــــــــــــ = ـــــــــــــ = ــــــــــــ = م
(1\15) (1\10) (1\12)
هذا يعنى أن النسبية بين اضلاع المثلث كـنسبة
(1\15) : (1\10) : (1\12) ، وبإستعمال قانون جيب
التمام نوجد قياس اصغر زاوية التى تقابل اصغر ضلع
وهى الزاوية جـ .
(ب جـ)² + (أ جـ)² - (أ ب)²
جتاجـ = ــــــــــــــــــــــــــــــــــــــــــ
2(ب جـ) (أ جـ)
(1\10)² + (1\12)² - (1\15)² 3
= ـــــــــــــــــــــــــــــــــــــــــــــــ = ـــــــــ
2(1\10)(1\12) 4
اذاً : جـ = جتا^-1(3\4) ≈ "34.64 '24 41ْ
اى : 41 درجة ، 24 دقيقة ، 34.64 ثانية .
15 أب = 10 ب جـ = 12 أجـ
أصغر ضلع هو أ ب لماذاً ؟ لأن اصغر ضلع
هو الذى معامله يكون أكبر .. كيف ذلك ؟
اذا قُلنا أن 1 دولار = 6 جنيه (تقريباً)
هذا يعنى أن الجنيه أقل من الدولار .
الضلع أب تقابله الزواية جـ ..
اذا كان هذا الشىء يبدو ساذجاً عندك فأسعمل
قوانين النسبة والتناسب :
نفرض أن : 15 أب = 10 ب جـ = 12 أجـ = م
حيث م = ثابت التناسب .
وهذا يدلنا على اننا يمكن أن نضع التناسب
السابق لكن فى صورة أخرى .....
أ ب ب جـ أ جـ
ــــــــــــ = ـــــــــــــ = ــــــــــــ = م
(1\15) (1\10) (1\12)
هذا يعنى أن النسبية بين اضلاع المثلث كـنسبة
(1\15) : (1\10) : (1\12) ، وبإستعمال قانون جيب
التمام نوجد قياس اصغر زاوية التى تقابل اصغر ضلع
وهى الزاوية جـ .
(ب جـ)² + (أ جـ)² - (أ ب)²
جتاجـ = ــــــــــــــــــــــــــــــــــــــــــ
2(ب جـ) (أ جـ)
(1\10)² + (1\12)² - (1\15)² 3
= ـــــــــــــــــــــــــــــــــــــــــــــــ = ـــــــــ
2(1\10)(1\12) 4
اذاً : جـ = جتا^-1(3\4) ≈ "34.64 '24 41ْ
اى : 41 درجة ، 24 دقيقة ، 34.64 ثانية .
0 كم عدد المستطيلات الموجودة بالشكل ؟
السبت، 25 أغسطس 2012
التسميات:
الجبر,
مواضيع متنوعة,
هندسة مستوية
 |
| افتح الصورة فى رابط مستقل |
على فرض ان جميع المستطيلات (المستقلة) المبينة بالشكل مختلفة ...
انظر الى ايمن المستطيل (او مستطيل صغير على يمين) .. ثبته لتجد
انه يضم فى الصف الواحد 10 مستطيلات، ثم نضم معه المستطيل
الذى تحته (ونثبتهم) لنجد انهم يضموا ايضاً 10 مستطيلات .. وهكذا
نخرج من هذه العملية (مع تثبيت المستطيل الصغير على اليمين)
بـ 10 × 9 = 90 مستطيل .
ثم نأتى الى المستطيل الثانى اعلى يمين المستطيل ونثبته لنجد
انه التحم مع 9 مستطيلات فى الصف الواحد، وهكذا مع عملية
التثبيت هذه نجد انه تكون لدينا 9 × 9 = 81 مستطيل .. وهكذا
نصنع مع كل مستطيل من الصف العلوى للمسطيل (الأب)
الخلاصة انه مع تثبيت مستطيل ما لا نتجه ابداً (به) نحو اليمين
او نحو الأعلى حتى لا نكرر مستطيلات نحن قد أخذناها بالفعل ...
(اى مع التثبيت نتوجه به شمالاً او اسفل فقط)
فيتكون لدينا هذه المتابعة البسيطة (متتابعة حسابية)
(10×9) + (9×9) + (8×9) + (7×9) + .... + (1×9)
بأخذ 9 عامل مشترك ...
10(10 + 1)
= 9(1 + 2 + 3 + ... +10) = 9 × ــــــــــــــــــــــــ
2
= 495 مستطيل
(لاحظ مجموع الأعداد من 1 الى 10 = 55)
ولكن هذا نتج مع تثبيت الصفط الأول، لذلك هذه العملية نكررها
مع الـ 9 صفوف، ولكن عندما ننزل الى صف جديد ينقص عدد
الأعمدة مقدار 1
اى مع تثبيت الصف الثانى نحصل على عدد مستطيلات وقدره
(10×8) + (9×8) + (8×8) + (7×8) + .... + (1×8)
= 8 × 55 = 440 مستطيل
ولكن هذا شىء ممل كثيراً نلاحظ انه فى كل مرة نثبت فيها
الصف تنقص الأعمدة بمقدار واحد ليتكون لدينا فى الأخير
هذا المجموع ..
(9×55) + (8×55) + (7×55) + ..... + (1×55)
= 55[1 + 2 + 3 + .... +9] = 55 × 45 = 2475 مستطيل
انظر الى ايمن المستطيل (او مستطيل صغير على يمين) .. ثبته لتجد
انه يضم فى الصف الواحد 10 مستطيلات، ثم نضم معه المستطيل
الذى تحته (ونثبتهم) لنجد انهم يضموا ايضاً 10 مستطيلات .. وهكذا
نخرج من هذه العملية (مع تثبيت المستطيل الصغير على اليمين)
بـ 10 × 9 = 90 مستطيل .
ثم نأتى الى المستطيل الثانى اعلى يمين المستطيل ونثبته لنجد
انه التحم مع 9 مستطيلات فى الصف الواحد، وهكذا مع عملية
التثبيت هذه نجد انه تكون لدينا 9 × 9 = 81 مستطيل .. وهكذا
نصنع مع كل مستطيل من الصف العلوى للمسطيل (الأب)
الخلاصة انه مع تثبيت مستطيل ما لا نتجه ابداً (به) نحو اليمين
او نحو الأعلى حتى لا نكرر مستطيلات نحن قد أخذناها بالفعل ...
(اى مع التثبيت نتوجه به شمالاً او اسفل فقط)
فيتكون لدينا هذه المتابعة البسيطة (متتابعة حسابية)
(10×9) + (9×9) + (8×9) + (7×9) + .... + (1×9)
بأخذ 9 عامل مشترك ...
10(10 + 1)
= 9(1 + 2 + 3 + ... +10) = 9 × ــــــــــــــــــــــــ
2
= 495 مستطيل
(لاحظ مجموع الأعداد من 1 الى 10 = 55)
ولكن هذا نتج مع تثبيت الصفط الأول، لذلك هذه العملية نكررها
مع الـ 9 صفوف، ولكن عندما ننزل الى صف جديد ينقص عدد
الأعمدة مقدار 1
اى مع تثبيت الصف الثانى نحصل على عدد مستطيلات وقدره
(10×8) + (9×8) + (8×8) + (7×8) + .... + (1×8)
= 8 × 55 = 440 مستطيل
ولكن هذا شىء ممل كثيراً نلاحظ انه فى كل مرة نثبت فيها
الصف تنقص الأعمدة بمقدار واحد ليتكون لدينا فى الأخير
هذا المجموع ..
(9×55) + (8×55) + (7×55) + ..... + (1×55)
= 55[1 + 2 + 3 + .... +9] = 55 × 45 = 2475 مستطيل
نستنتج : انه اذا كان عدد الصفوف ص وعدد الأعمد ع
فإن عدد المستطيلات الممكنة :
ص ع
= سيجما ك × سيجما ك
ك=1 ك=1
ص(ص+1) ع(ع+1)
= ـــــــــــــــــــــ × ــــــــــــــــــــــ
2 2
ص ع (ص+1) (ع+1)
= ــــــــــــــــــــــــــــــــــــــــــــ
4
اى :
عدد الصفوف×عدد الأعمدة×(عدد الصفوف+1)×(عدد الأعمدة+1)
=ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
4
فى مثالنا نقول : عدد الصفوف = 10 ، عدد الأعمدة = 9
9 × 10 × 11 × 10
عدد المستطيلات = ــــــــــــــــــــــــــــــــ = 2475 مستطيل
4
فإن عدد المستطيلات الممكنة :
ص ع
= سيجما ك × سيجما ك
ك=1 ك=1
ص(ص+1) ع(ع+1)
= ـــــــــــــــــــــ × ــــــــــــــــــــــ
2 2
ص ع (ص+1) (ع+1)
= ــــــــــــــــــــــــــــــــــــــــــــ
4
اى :
عدد الصفوف×عدد الأعمدة×(عدد الصفوف+1)×(عدد الأعمدة+1)
=ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
4
فى مثالنا نقول : عدد الصفوف = 10 ، عدد الأعمدة = 9
9 × 10 × 11 × 10
عدد المستطيلات = ــــــــــــــــــــــــــــــــ = 2475 مستطيل
4
0 كيفية ايجاد مساحة الدائرة الداخلة للمثلث ؟
الخميس، 19 يوليو 2012
التسميات:
هندسة مستوية
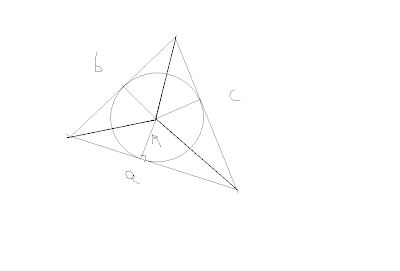
لدينا في المثلث نقطة تقاطع المنصفات هي مركز الدائرة التي داخل المثلث
السؤال هو كيف نحسب مساحة هذه الدائرة؟ هل يوجد قانون اوشيء ما يساعد في حساب مساحتها؟
علما ان نصف قطرها مجهول، والمعلوم هو اطوال المثلث .
السؤال هو كيف نحسب مساحة هذه الدائرة؟ هل يوجد قانون اوشيء ما يساعد في حساب مساحتها؟
علما ان نصف قطرها مجهول، والمعلوم هو اطوال المثلث .
لك فقط ان تعلم قاعدة هيرون لإيجاد مساحة
المثلث بدلالة أطوال أضلاعه، فإذا كانت أطوال أضلاع المثلث (اى مثلث)
هى a , b , c فإن مساحته هى : A = sqrt[s(s-a)(s-b)(s-c)] l
حيث s = (a+b+b)/2 أو بإختصار s هى نصف محيط المثلث، .
(اثبات مفصل لقاعدة هيرون)
ننتقل الآن الى سؤالنا : فكما أنك قلت ان الدائرة الداخلة للمثلث مركزها هو
نقطة تلاقى منصفات هذا المثلث، فإنه ايضاً من الضرورى ان تعلم ان نفس هذه
النقطة (مركز الدائرة) هى نقطة تلاقة انصاف أقطار الدائرة (حقيقة)، ومن ضمن
هذه الأنصاف اقطار التى تكون عمودى على المماس (المماسات هنا أضلاع المثلث)
نظرية : نصف القطر عمود على المماس .
فكرة الحل بسيطة جداً وهى ننا لو علمنا نصف قطر الدائرة لأوجدنا مساحتها .
الآن نعلم ان مساحة المثلث (بقاعدة هيرون) هى :
A = sqrt[s(s-a)(s-b)(s-c)] l
ولكن يمكن ايجاد مساحة المثلث بطريقة أخرى (او كام هو موضح بالرسم)
مساحة المثلث = مساحة ثلاث مثلثات جميع ارتفاعتها (نصف قطر الدائرة)
مساحة المثلث = ½ القاعدة × الإرتفاع .
والآن بعد تقسيم المثلث (المحيط بالدائرة) الى ثلاث مثلثات نستطيع ان نوجد A
بطريقة أخرى وهى :
A = ½ar + ½br + ½cr = r(a+b+c)/2 = rs
اذاً : rs = sqrt[s(s-a)(s-b)(s-c)] l بتربيع الطرفين ..
r²s² = s(s-a)(s-b)(s-c) l بقسمة الطرفين على s²
r² = (s-a)(s-b)(s-c)/s بضرب الطرفين فى pi (النسبة التقريبية)
pi r² = pi(s-a)(s-b)(s-c)/s
مثال : اذا كانت أضلاع المثلث هى : 9 , 7 , 5
s = (5+7+9)/2 = 10.5 وبالتالى فإن :
Area of circle = pi (10.5 - 5)(10.5 - 7)(10.5 - 9)/10.5 = 11pi/4 ≈ 8.64
المثلث بدلالة أطوال أضلاعه، فإذا كانت أطوال أضلاع المثلث (اى مثلث)
هى a , b , c فإن مساحته هى : A = sqrt[s(s-a)(s-b)(s-c)] l
حيث s = (a+b+b)/2 أو بإختصار s هى نصف محيط المثلث، .
(اثبات مفصل لقاعدة هيرون)
ننتقل الآن الى سؤالنا : فكما أنك قلت ان الدائرة الداخلة للمثلث مركزها هو
نقطة تلاقى منصفات هذا المثلث، فإنه ايضاً من الضرورى ان تعلم ان نفس هذه
النقطة (مركز الدائرة) هى نقطة تلاقة انصاف أقطار الدائرة (حقيقة)، ومن ضمن
هذه الأنصاف اقطار التى تكون عمودى على المماس (المماسات هنا أضلاع المثلث)
نظرية : نصف القطر عمود على المماس .
فكرة الحل بسيطة جداً وهى ننا لو علمنا نصف قطر الدائرة لأوجدنا مساحتها .
الآن نعلم ان مساحة المثلث (بقاعدة هيرون) هى :
A = sqrt[s(s-a)(s-b)(s-c)] l
ولكن يمكن ايجاد مساحة المثلث بطريقة أخرى (او كام هو موضح بالرسم)
مساحة المثلث = مساحة ثلاث مثلثات جميع ارتفاعتها (نصف قطر الدائرة)
مساحة المثلث = ½ القاعدة × الإرتفاع .
والآن بعد تقسيم المثلث (المحيط بالدائرة) الى ثلاث مثلثات نستطيع ان نوجد A
بطريقة أخرى وهى :
A = ½ar + ½br + ½cr = r(a+b+c)/2 = rs
اذاً : rs = sqrt[s(s-a)(s-b)(s-c)] l بتربيع الطرفين ..
r²s² = s(s-a)(s-b)(s-c) l بقسمة الطرفين على s²
r² = (s-a)(s-b)(s-c)/s بضرب الطرفين فى pi (النسبة التقريبية)
pi r² = pi(s-a)(s-b)(s-c)/s
مثال : اذا كانت أضلاع المثلث هى : 9 , 7 , 5
s = (5+7+9)/2 = 10.5 وبالتالى فإن :
Area of circle = pi (10.5 - 5)(10.5 - 7)(10.5 - 9)/10.5 = 11pi/4 ≈ 8.64
0 كيفية حساب المساحة السطحية للكرة ؟
الأحد، 1 يوليو 2012
التسميات:
التفاضل والتكامل,
هندسة فراغية,
هندسة مستوية
تستطيع ان توجد مساحة الكرة من خلال مساحة الجسم الناتج عن دوران نصف
دائرة (تمر بنقطة الأصل) نصف قطرها نق عن طريقة التكامل المحدود ..
نفرض أن الدائرة هى : س²+ص² = نق²
ومنها : ص = جذر(نق² - س²) اخذنا الحل الموجب فقط ...
أ
قانون حساب مساحة الجسم الدورانى : 2ط ∫د(س) دم
ب
حيث : دم = جذر[1+دَ(س)²] دس
لذللك نوجد أولاً مشتقة الدالة ...
- س
دَ(س) = ــــــــــــــــــــــــــــ نقوم بالتربيع واضافة 1
جذر(نق² - س²)
س² نق²
ـــــــــــــــــــــ + 1 = ــــــــــــــــــــــ
نق² - س² نق² - س²
نق
اذاً : دم = ــــــــــــــــــــــــــــ دس
جذر(نق² - س²)
التكامل لحساب مساحة الكرة هو (تكامل محدود من -نق الى نق)
نق نق
= 2ط∫ جذر(نق² - س²) × ــــــــــــــــــــــــــ دس
-نق جذر(نق² - س²)
نق نق
= 2ط ∫ نق دس = 2ط [نق س] = 2ط نق [نق - (-نق)]
-نق -نق
= 2ط نق × 2نق = 4 ط نق²
دائرة (تمر بنقطة الأصل) نصف قطرها نق عن طريقة التكامل المحدود ..
نفرض أن الدائرة هى : س²+ص² = نق²
ومنها : ص = جذر(نق² - س²) اخذنا الحل الموجب فقط ...
أ
قانون حساب مساحة الجسم الدورانى : 2ط ∫د(س) دم
ب
حيث : دم = جذر[1+دَ(س)²] دس
لذللك نوجد أولاً مشتقة الدالة ...
- س
دَ(س) = ــــــــــــــــــــــــــــ نقوم بالتربيع واضافة 1
جذر(نق² - س²)
س² نق²
ـــــــــــــــــــــ + 1 = ــــــــــــــــــــــ
نق² - س² نق² - س²
نق
اذاً : دم = ــــــــــــــــــــــــــــ دس
جذر(نق² - س²)
التكامل لحساب مساحة الكرة هو (تكامل محدود من -نق الى نق)
نق نق
= 2ط∫ جذر(نق² - س²) × ــــــــــــــــــــــــــ دس
-نق جذر(نق² - س²)
نق نق
= 2ط ∫ نق دس = 2ط [نق س] = 2ط نق [نق - (-نق)]
-نق -نق
= 2ط نق × 2نق = 4 ط نق²
0 حل تمرين فى القطع المكافىء ..
الخميس، 28 يونيو 2012
التسميات:
هندسة تحليلية,
هندسة مستوية
ليكن P القطع المكافئ الذي معادلته x²=2y و ليكن [pQ] و ترا محرقيا فيه ميله m ( اي p و Q هما نقطتا تقاطع مستقيم ميله m مار بمحرق القطع )
1 - أثبت ان المماسين في p و Q للقطع P متعامدان
2 - أثبن ان المماسين في p , Q يتقاطعان في نقطة تقع على دليل P
3 - هل تبقى الخاصتان السابقتان صحيحتين في حالة اي قطع مكافئ
التمرين موجود في صفحة 93 تمرين رقم 2 (الهندسة التحليلية)
و ارجو ان تكون الإجابة مفصلة بشكل دقيق جدا و لو مع الرسم
1 - أثبت ان المماسين في p و Q للقطع P متعامدان
2 - أثبن ان المماسين في p , Q يتقاطعان في نقطة تقع على دليل P
3 - هل تبقى الخاصتان السابقتان صحيحتين في حالة اي قطع مكافئ
التمرين موجود في صفحة 93 تمرين رقم 2 (الهندسة التحليلية)
و ارجو ان تكون الإجابة مفصلة بشكل دقيق جدا و لو مع الرسم
معادة القطع المكافىء هى : س² = 2ص (نضعها على الصورة القياسية)
اذاً : س² = 4 × ½ص اى ان أ = ½ وهى المسافة بين رأس القطع المكافىء
وبؤرته او بين الرأس ودليله .. من هنا نستخلص ما يلى .
معادلة دليله هى : ص = -½ احداثيات بؤرته (محرقه) هى : (0 ، ½)
المستقيمات المارة من محرقة تقطع محور الصادات فى ½ اذا الصورة
القياسية لجميع هذه المستقيمات هى : ص = م س + ½ حيث م
هى الميل المتغير لهذه المستقيمات ...
أولاً نوجد نقطة تقاطع القطع المكافىء مع المستقيم ص = م س + ½ بأن
نقوم بحلهم معاً .... بالتعويض فى معادلة القطع عن : ص = م س + ½
س² = 2(م س + ½) ومنها س² = 2 م س + 1 (نحل المعادلة فى س)
س² - 2 م س - 1 = 0 نحل المقدار الثلاثى بالقانون العام .....
المميز(او دلتا) = 4م² - 4(-1) = 4(م²+1)
2م + 2جذر(م²+1)
س = ــــــــــــــــــــــــــــــــ = م+جذر(م²+1)
2
أو : س = م - جذر(م²+1)
الآن وبكل بساطة ويسر يريد ميل المماس (فى القطع المكافىء) عند هذه الإحداثيات ..
س² = 2ص ومنها ص = ½س² (نشتق الطرفين بالنسبة لـ س)
صَ = س او تكتب هكذا دَ(س) = س
دَ(م+جذر(م²+1)) = م+جذر(م²+1)
دَ(م - جذر(م²+1)) = م - جذر(م²+1)
بضرب الميل الاول × الثانى
[م+جذر(م²+1)][م - جذر(م²+1)] = م² - (م²+1) = -1
اذاً المماسان متعامدان (لأن حصاصل ضرب الميلين المتعامدين = -1)
نفرض أن معادلة المماس الأول : ص = [م+جذر(م²+1)]س + ب
معادلة المماس الثانى : ص = [م - جذر(م²+1)]س + جـ
حيث ب ، جـ الأجزاء المقطوعة من محور الصادات ... بحل المماسين معاً ينتج لنا
نقطع تقاطع المماسين (والتى نريد ان نتحقق هل بالفعل تقع على دليل القطع ؟ )
ص = [م+جذر(م²+1)]س + ب (1)
ص = [م - جذر(م²+1)]س + جـ (2)
بضرب س فى القوس ينتج لنا ...
ص = م س +جذر(م²+1)س + ب (1)
ص = م س - جذر(م²+1)س + جـ (2)
بجمع (1) ، (2)
2ص = 2 م س + (ب+جـ) (3)
بطرح (1) ، (2)
0 = 2جذر(م²+1) س + (ب - جـ) (4)
ومنها 2جذر(م²+1) س = (جـ - ب)
(جـ - ب)
اذاً : س = ــــــــــــــــــــــــ بالتعويض فى معادلة (3)
2جذر(م²+1)
م (جـ - ب)
2ص = ـــــــــــــــــــــــــــ + (جـ+ب)
جذر(م²+1)
كيف نوجد ب ، جـ ؟
من خلال نقطتى ميل المماس للدالة ..
س = م+جذر(م²+1) او س = م - جذر(م²+1) بالتعويض فى معادلة القطع ..
د(س) = ½س² ومنها د(م+جذر(م²+1)) = ½[م+جذر(م²+1)]²
وبالمثل : د(م - جذر(م²+1)) = ½[م - جذر(م²+1)]²
بالتعويض بـ النقطة (م+جذر(م²+1) ، ½[م+جذر(م²+1)]²) فى المماس الأول ..
ص = [م+جذر(م²+1)]س + ب
½[م+جذر(م²+1)]² = [م+جذر(م²+1)][(م+جذر(م²+1)] + ب
ب = ½[م+جذر(م²+1)]² - [م+جذر(م²+1)][(م+جذر(م²+1)]
= ½[م+جذر(م²+1)]² - [م+جذر(م²+1)]² = -½[م+جذر(م²+1)]²
بنفس الطريقة نوجد جـ .. عوض بالنقطة (م - جذر(م²+1) ، ½[م - جذر(م²+1)]²)
فى المماس الثانى .. ص = [م - جذر(م²+1)]س + جـ
½[م - جذر(م²+1)]² = [م - جذر(م²+1)] [م - جذر(م²+1)] + جـ
اذاً : جـ = ½[م - جذر(م²+1)]² - [م - جذر(م²+1)] [م - جذر(م²+1)]
= ½[م - جذر(م²+1)]² - [م - جذر(م²+1)]² = -½[م - جذر(م²+1)]²
الآن نوجد كلاً من جـ +ب ، جـ - ب
جـ+ب = -½[م - جذر(م²+1)]² - ½[م+جذر(م²+1)]²
= -½ [ [م - جذر(م²+1)]² + [م+جذر(م²+1)]² ]
= -½ [م² - 2م جذر(م²+1) + (م²+1) + م² + 2م جذر(م²+1)+ (م²+1) ]
= -½(4م²+2) = - (2م²+1)
ثانياً ايجاد : جـ - ب
جـ - ب = -½[م - جذر(م²+1)]² + ½[م+جذر(م²+1)]²
= -½[ [م - جذر(م²+1)]² - [م+جذر(م²+1)]² ]
= -½ [ م² - 2م جذر(م²+1) + (م²+1) - م² -2م جذر(م²+1) - (م²+1)]
= -½[-4م جذر(م²+1)] = 2م جذر(م²+1)
بالتعويض فى :
م (جـ - ب)
2ص = ـــــــــــــــــــــــــــ + (جـ+ب)
جذر(م²+1)
2م² جذر(م²+1)
اذاً : 2ص = ــــــــــــــــــــــــــــ - (2م²+1) = 2م² - 2م² - 1 = -1
جذر(م²+1)
ص = -½ ولكن هذه معادلة دليل القطع المكافىء
اذاً المطلوب الثانى تحقق ...
4 اثبت ان منصفات المثلثات تتلاقى فى نقطة واحدة بنسبة 2 : 1 من جهة الرأس و 1 : 2 من جهة القاعدة ؟
الأربعاء، 27 يونيو 2012
التسميات:
هندسة مستوية
هناك طريقة استنتجتها، ومفهومها سهل وبسيط ..
فى المثلث أ ب جـ عبرت عن نقطة تلاقى متوسطات المثلثات بـ " و "
فى الإثبات سأستعمل النظريات الآتية (واذا اردتى اثبات كل نظرية منها فليس عندى مانع) :
1) متوسط اى مثلث يقسمه الى مثلثين متساويين فى المساحة .
2) جا(الزاوية) = جا(الزاوية المكملة لها)
مثال : جا(30) = جا(180 - 30) = جا150 وهكذا ..
3) مساحة المثلث (حسب مفهوم حساب المثلثات) =
½ حاصل ضرب طولى اى ضلعين × جيب الزاوية المحصورة بينهما
4) نقطة تلاقى متوسطات المثلث تتقابل فى نقطة واحدة داخله " النقطة و "
.............................................................................................
الإثبات : فى المثلث أ ب جـ فيه ب ص ينصف القاعدة أ جـ .. اذاً
مساحة المثلث ب أ ص = مساحة المثلث ب جـ ص
ولكن و ص منصف للمثلث و أ جـ اذاً مساحة أ و ص = مساحة جـ و ص
اذاً : مساحة المثلث أ و ب = مساحة المثلث و ب جـ كيف تم ذلك ؟
"سأضرب مثل سريع : اذا كان معك حقيبتين بهما اموال الأولى بها مليون دولار والثانية
ايضاً تحتوى على مليون دولار (اى ان الحقيبة الأولى = الحقيبة الثانية)
.. اخذنا من الحقيبة الأولى 100 الف دولار ومن الحقيبة الثانية 100 الف دولار فهل
الحقيبة الأولى = الحقيبة الثانية ؟ .. اظن الإجابة واضحة جداً "
وصلنا الى : مساحة المثلث أ و ب = مساحة المثلث و ب جـ
ولكن و س منصف للقاعدة أ ب اذاً مساحة أ و س = مساحة و س ب
وايضاً : و د منصف للقاعدة ب جـ اذاً مساحة و ب د = و د جـ
مما سبق ينتج أن : مساحة أ س و = مساحة س و ب = مساحة و ب د
أو : مساحة أ ب و = 2×مساحة و ب د
اى أن : ½ أ و × ب و × جا(أ و ب) = 2×½ ب و × و د × جا(ب و د)
بإختصار ½ ب و من الطرفين ....
أ و × جا(أ و ب) = 2 و د × جا(ب و د)
ولكن : الزاوية أ و د مستقيمة = 180 اى ان الزاوية أ و ب تكمل الزاوية ب و د
وبالتالى : جا(أ و ب) = جا( ب و د) (نختصرها من الطرفين ...) ينتج لنا
أ و = 2 و د (وهو المطلوب اثباته)
((طبعاً بنفس الطريقة نطبق البرهان على المنصفين الآخرين فى المثلث))
فى المثلث أ ب جـ عبرت عن نقطة تلاقى متوسطات المثلثات بـ " و "
فى الإثبات سأستعمل النظريات الآتية (واذا اردتى اثبات كل نظرية منها فليس عندى مانع) :
1) متوسط اى مثلث يقسمه الى مثلثين متساويين فى المساحة .
2) جا(الزاوية) = جا(الزاوية المكملة لها)
مثال : جا(30) = جا(180 - 30) = جا150 وهكذا ..
3) مساحة المثلث (حسب مفهوم حساب المثلثات) =
½ حاصل ضرب طولى اى ضلعين × جيب الزاوية المحصورة بينهما
4) نقطة تلاقى متوسطات المثلث تتقابل فى نقطة واحدة داخله " النقطة و "
.............................................................................................
الإثبات : فى المثلث أ ب جـ فيه ب ص ينصف القاعدة أ جـ .. اذاً
مساحة المثلث ب أ ص = مساحة المثلث ب جـ ص
ولكن و ص منصف للمثلث و أ جـ اذاً مساحة أ و ص = مساحة جـ و ص
اذاً : مساحة المثلث أ و ب = مساحة المثلث و ب جـ كيف تم ذلك ؟
"سأضرب مثل سريع : اذا كان معك حقيبتين بهما اموال الأولى بها مليون دولار والثانية
ايضاً تحتوى على مليون دولار (اى ان الحقيبة الأولى = الحقيبة الثانية)
.. اخذنا من الحقيبة الأولى 100 الف دولار ومن الحقيبة الثانية 100 الف دولار فهل
الحقيبة الأولى = الحقيبة الثانية ؟ .. اظن الإجابة واضحة جداً "
وصلنا الى : مساحة المثلث أ و ب = مساحة المثلث و ب جـ
ولكن و س منصف للقاعدة أ ب اذاً مساحة أ و س = مساحة و س ب
وايضاً : و د منصف للقاعدة ب جـ اذاً مساحة و ب د = و د جـ
مما سبق ينتج أن : مساحة أ س و = مساحة س و ب = مساحة و ب د
أو : مساحة أ ب و = 2×مساحة و ب د
اى أن : ½ أ و × ب و × جا(أ و ب) = 2×½ ب و × و د × جا(ب و د)
بإختصار ½ ب و من الطرفين ....
أ و × جا(أ و ب) = 2 و د × جا(ب و د)
ولكن : الزاوية أ و د مستقيمة = 180 اى ان الزاوية أ و ب تكمل الزاوية ب و د
وبالتالى : جا(أ و ب) = جا( ب و د) (نختصرها من الطرفين ...) ينتج لنا
أ و = 2 و د (وهو المطلوب اثباته)
((طبعاً بنفس الطريقة نطبق البرهان على المنصفين الآخرين فى المثلث))
1 اثبت ان مساحة القطاع الدائرى = ½نق² هـ
الاثنين، 18 يونيو 2012
التسميات:
حساب مثلثات,
مواضيع متنوعة,
هندسة مستوية
نعلم ان : ل
ـــــــــــــ = هـ
نق
حيث ل = طول القوس ، نق = نصف قطر الدائرة ، هـ = قياس الزاوية بالتقدير الدائرى .
ومنها : ل = هـ × نق
الآن فى الرسم فى المراجع قمت بتقسيم القطاع الدائرى الى عدد لا نهائى
من المثلثات المتساوية الساقين، بحيث كل ساق = نق
مساحة المثلث = ½ القاعدة × الإرتفاع
وعندما تقون هذه المثلثات كثيرة جداً فإننا لا نفرق وقتها بين نق وبين
ارتفاع المثلث ..
نفرق اننا قسمنا قوس القطاع الى ل0 ، ل1 ، ل2 ، ل3 ، ..... الخ
مساحة المثلث الأول = ½ل0 نق
مساحة المثلث الثانى = ½ل1 نق .. وهكذا
مساحة جميع هذه المثلثات = مساحة القطاع الدائرى
= ½ل0 نق + ½ل1 نق + ½ل2 نق + .......
بأخذ ½نق عامل مشترك ...
= ½نق (ل0+ل1+ل2+ل3+.....)
ولكن (ل0+ل1+ل2+ل3+.....) = طول القوس = ل اذاً
مساحة القطاع الدائرى = ½ل نق
ولكن ل = هـ×نق بالتعويض ..
اذاً : مساحة القطاع الدائرى = ½×هـ×نق×نق = ½نق² هـ
حيث هـ قياس الزاوية المركزبة (للقطاع الدائرى) بالتقدير الدائرى .
ـــــــــــــ = هـ
نق
حيث ل = طول القوس ، نق = نصف قطر الدائرة ، هـ = قياس الزاوية بالتقدير الدائرى .
ومنها : ل = هـ × نق
الآن فى الرسم فى المراجع قمت بتقسيم القطاع الدائرى الى عدد لا نهائى
من المثلثات المتساوية الساقين، بحيث كل ساق = نق
مساحة المثلث = ½ القاعدة × الإرتفاع
وعندما تقون هذه المثلثات كثيرة جداً فإننا لا نفرق وقتها بين نق وبين
ارتفاع المثلث ..
نفرق اننا قسمنا قوس القطاع الى ل0 ، ل1 ، ل2 ، ل3 ، ..... الخ
مساحة المثلث الأول = ½ل0 نق
مساحة المثلث الثانى = ½ل1 نق .. وهكذا
مساحة جميع هذه المثلثات = مساحة القطاع الدائرى
= ½ل0 نق + ½ل1 نق + ½ل2 نق + .......
بأخذ ½نق عامل مشترك ...
= ½نق (ل0+ل1+ل2+ل3+.....)
ولكن (ل0+ل1+ل2+ل3+.....) = طول القوس = ل اذاً
مساحة القطاع الدائرى = ½ل نق
ولكن ل = هـ×نق بالتعويض ..
اذاً : مساحة القطاع الدائرى = ½×هـ×نق×نق = ½نق² هـ
حيث هـ قياس الزاوية المركزبة (للقطاع الدائرى) بالتقدير الدائرى .
0 اثبت ان الدائرتين متماستان مبياً نوع التماس
الاثنين، 11 يونيو 2012
التسميات:
هندسة مستوية
س²+ص²-2س+4ص-11=0 ، (س-7)² + (ص-6)² = 36
الجل : لكى نثبت ان الدائرتين المذكورتين فى السؤال متماستان
يجب ان نثبت ان معادلة المماس للدائرة الأولى ومعادلة
المماس للدائرة الثانية مشتركان فى نقطة وحيدة وهى
نقطة التماس (اى نحلهم معاً) .. طبعاً هذه طريقة
ويوجد طريقة أخرى مباشرة بأن تقوم بحلهم من الآن
(بدون اشتقاق) بحيث نثبت ان لهم حل وحيد وهى
نقطة التماس .. ولكننا سنحل بالطريقة الأولى ..
س²+ص²-2س+4ص-11=0 --------> (1)
(س-7)² + (ص-6)² = 36 فك المعادلة ..
س² - 14س + 49 + ص² - 12ص + 36 = 36
س²+ص²-14س-12ص+49=0 --------> (2)
بطرح (2) من (1)
12س+16ص = 60 بقسمة الطرفين على 4
3س+4ص = 15
15 - 3س
4ص = 15 - 3س ومنها ص = ـــــــــــــــــــ --------> (3)
4
بالتعويض فى معادلة (1)
س²+ص²-2س+4ص-11=0 --------> (1)
(15 - 3س)²
س² + ـــــــــــــــــــــ - 2س + 15 - 3س - 11 = 0
16
(15 - 3س)²
س² + ـــــــــــــــــــــ - 5س + 4 = 0
16
بضرب لطرفين فى 16 ..
16س² + (15 - 3س)² - 80س + 64 = 0
16س² + 225 - 90س + 9س² - 80س + 64 = 0
25س² - 170س + 289 = 0
المميز = [(170)² - (4×25×289)] = 0
وهذا يدل على انه يوجد حل وحيد فقط للدائرتين معاً وهى نقطة التماس
(( أكمل حل المعادلة بالقانون العام))
170
س = ــــــــــــــــــ = 3.4 بالتعويض فى معادلة (3)
2 × 25
15 - 3س
ص = ـــــــــــــــــــ --------> (3)
4
15 - 3(3.4)
ص = ــــــــــــــــــــــ = 1.2
4
اذاً نقطة التماس هى (3.4 ، 1.2)
اذا كان التماس من الخاجر فإن طول القطعة المستقيمة
الواصلة بين مركزى الدائرتين = مجموع انصاف اقطارهم
وهذا ما سنثبته .. نقوم بإكمال المربع أولاً فى الدائرة الأولى
س²+ص²-2س+4ص-11=0
س² - 2س + ص² + 4ص -11 = 0
لكى نكمل المربع لكلاً من حدودية س ، ص
فإننا نحتاج الحد الثالث والذى = (½ معامل الحد الخالى من تربيع)²
مثلاً : س² - 2س كيف نوجد الحد الثالث ؟
(½ × -2)² = (-1)² = 1
بالمثل : ص² + 4ص الحد الثالث = (½×4)² = 4
والآن نقوم بإضافة 1 + 4 = 5 وطرحها مرة أخرى ..
س² - 2س + 1 + ص² + 4ص + 4 - 5 - 11 = 0
(س-1)² + (ص+2)² = 16
اذاً مركز الدائرة هو : (1 ، -2) ونصف قطرها = 4
الدائرة الثانية : (س-7)² + (ص-6)² = 36
مركزها (7 ، 6) ونصف قطرها = 6
مجموع نق1+ق2 = 4 + 6 = 10
الآن بقانون البعد بين نقطتين نوجد طول القطعة المستقيمة
بين النقتطين (7 ، 6) ، (1 ، -2)
= جذر[(7 - 1)² + (6 - -2)²] = جذر(100) = 10
اذاً نوع التماس (من الخارج)
الجل : لكى نثبت ان الدائرتين المذكورتين فى السؤال متماستان
يجب ان نثبت ان معادلة المماس للدائرة الأولى ومعادلة
المماس للدائرة الثانية مشتركان فى نقطة وحيدة وهى
نقطة التماس (اى نحلهم معاً) .. طبعاً هذه طريقة
ويوجد طريقة أخرى مباشرة بأن تقوم بحلهم من الآن
(بدون اشتقاق) بحيث نثبت ان لهم حل وحيد وهى
نقطة التماس .. ولكننا سنحل بالطريقة الأولى ..
س²+ص²-2س+4ص-11=0 --------> (1)
(س-7)² + (ص-6)² = 36 فك المعادلة ..
س² - 14س + 49 + ص² - 12ص + 36 = 36
س²+ص²-14س-12ص+49=0 --------> (2)
بطرح (2) من (1)
12س+16ص = 60 بقسمة الطرفين على 4
3س+4ص = 15
15 - 3س
4ص = 15 - 3س ومنها ص = ـــــــــــــــــــ --------> (3)
4
بالتعويض فى معادلة (1)
س²+ص²-2س+4ص-11=0 --------> (1)
(15 - 3س)²
س² + ـــــــــــــــــــــ - 2س + 15 - 3س - 11 = 0
16
(15 - 3س)²
س² + ـــــــــــــــــــــ - 5س + 4 = 0
16
بضرب لطرفين فى 16 ..
16س² + (15 - 3س)² - 80س + 64 = 0
16س² + 225 - 90س + 9س² - 80س + 64 = 0
25س² - 170س + 289 = 0
المميز = [(170)² - (4×25×289)] = 0
وهذا يدل على انه يوجد حل وحيد فقط للدائرتين معاً وهى نقطة التماس
(( أكمل حل المعادلة بالقانون العام))
170
س = ــــــــــــــــــ = 3.4 بالتعويض فى معادلة (3)
2 × 25
15 - 3س
ص = ـــــــــــــــــــ --------> (3)
4
15 - 3(3.4)
ص = ــــــــــــــــــــــ = 1.2
4
اذاً نقطة التماس هى (3.4 ، 1.2)
اذا كان التماس من الخاجر فإن طول القطعة المستقيمة
الواصلة بين مركزى الدائرتين = مجموع انصاف اقطارهم
وهذا ما سنثبته .. نقوم بإكمال المربع أولاً فى الدائرة الأولى
س²+ص²-2س+4ص-11=0
س² - 2س + ص² + 4ص -11 = 0
لكى نكمل المربع لكلاً من حدودية س ، ص
فإننا نحتاج الحد الثالث والذى = (½ معامل الحد الخالى من تربيع)²
مثلاً : س² - 2س كيف نوجد الحد الثالث ؟
(½ × -2)² = (-1)² = 1
بالمثل : ص² + 4ص الحد الثالث = (½×4)² = 4
والآن نقوم بإضافة 1 + 4 = 5 وطرحها مرة أخرى ..
س² - 2س + 1 + ص² + 4ص + 4 - 5 - 11 = 0
(س-1)² + (ص+2)² = 16
اذاً مركز الدائرة هو : (1 ، -2) ونصف قطرها = 4
الدائرة الثانية : (س-7)² + (ص-6)² = 36
مركزها (7 ، 6) ونصف قطرها = 6
مجموع نق1+ق2 = 4 + 6 = 10
الآن بقانون البعد بين نقطتين نوجد طول القطعة المستقيمة
بين النقتطين (7 ، 6) ، (1 ، -2)
= جذر[(7 - 1)² + (6 - -2)²] = جذر(100) = 10
اذاً نوع التماس (من الخارج)
4 ايجاد مساحة القطعة الدائرية
الخميس، 24 مايو 2012
التسميات:
هندسة مستوية
نصف قطر الدائرة = نق
د هى قياس الزاوية بالتقدير الدائرى
العلاقة التى تربط بين التقدير الدائرة وطول القوس
ونصف قطر الدائرة هى :
ل/نق = د ومنها ل = د نق
حيث ل = طول القوس ..
مساحة القطعة الدائرية = مساحة القطاع الدائرى
- مساحة المثلث المتساوى الساقين الناشىء على الوتر
مساحة القطاع الدائرى = ½ل نق = ½ د نق × نق
= ½ د نق²
مساحة المثلث = ½حاصل ضرب الضلعين×جيب الزاوية المحصور بينهما
= ½ نق² جاد
والآن : مساحة القطعة الدائرية :
= ½ د نق² - ½ نق² جاد
بأخذ ½نق² عامل مشترك ..
= ½نق² (د - جاد)
حيث د قياس الزاوية المركزية بالتقدير الدائرى ..
الآن اذا أعطاك نق والزاوية .. اذاً ومباشرة ً استخدم
الصيغة أعلاه : المساحة = ½نق² (د - جاد)
واذا اعطاك نق والوتر ، او الزاوية والوتر فيمكنك استخدما
نفس القانون، ولكن تحتاج الى ايجاد العلاقة التى تربط
بين الوتر ونصف القطر والزواية بالرديان .. وتوجدها عن
طريق استعمالك لقانون جيب التمام .. نفرض أن طول
الوتر س .. اذاً
س² = نق²+نق² - 2نق×نق جتاد
= 2نق² - 2نق² جتاد = نق² (2 - 2جتاد)
اذاً س = نق جذر(2 - 2 جتاد)
0 اثبت ان النسبة بين مساحتى مثلثين متشابهين كنسبة مربع طولى أى ضلعين متناظرين
الخميس، 19 أبريل 2012
التسميات:
هندسة مستوية
نفرض أن نسبة التشابه كنسبة ك : م
بما أن المثلثان أ ب جـ ، د هـ و متشابهان اذاً :-
أب ب جـ أجـ ك
ــــــــــــ = ــــــــــــ = ـــــــــــ = ـــــــــــ
دهـ هـ و دو م
تذكر : مساحة المثلث = ½ حاصل ضرب أى ضلعين فى
جيب الزاوية المحصورة بينهما :
مساحة أ ب جـ = ½ أب × أ جـ × جاأ
مساحة د هـ و = ½ دهـ × دو × جاد
بقسمة المساحيتين :
ولاحظ ان جاأ = جاد لأن زاوية أ = زاوية د
نظراً لتشابه المثلثان .. وبناء عليه
½ أب × أ جـ × جاأ أب × أ جـ
= ــــــــــــــــــــــــــــــــــ = ـــــــــــــــــــــ
½ دهـ × دو × جاد دهـ × دو
ولكن فى أول الإجابة قلنا من التشابه ينتج أن :
أب ك أجـ ك
ــــــــــــ = ــــــــــ ، ــــــــــ = ــــــــــ
دهـ م دو م
أب × أ جـ ك ك ك
اذاً : ــــــــــــــــــ = ــــــــــ × ـــــــــ = [ــــــــ]²
دهـ × دو م م م
هذا يكافئ أن فى المثلين المتشابهين النسبة بين
مساحتى المثلثين كالنسبة بين مربع طولى أى ضلعين
متناظرين فيهما .
بما أن المثلثان أ ب جـ ، د هـ و متشابهان اذاً :-
أب ب جـ أجـ ك
ــــــــــــ = ــــــــــــ = ـــــــــــ = ـــــــــــ
دهـ هـ و دو م
تذكر : مساحة المثلث = ½ حاصل ضرب أى ضلعين فى
جيب الزاوية المحصورة بينهما :
مساحة أ ب جـ = ½ أب × أ جـ × جاأ
مساحة د هـ و = ½ دهـ × دو × جاد
بقسمة المساحيتين :
ولاحظ ان جاأ = جاد لأن زاوية أ = زاوية د
نظراً لتشابه المثلثان .. وبناء عليه
½ أب × أ جـ × جاأ أب × أ جـ
= ــــــــــــــــــــــــــــــــــ = ـــــــــــــــــــــ
½ دهـ × دو × جاد دهـ × دو
ولكن فى أول الإجابة قلنا من التشابه ينتج أن :
أب ك أجـ ك
ــــــــــــ = ــــــــــ ، ــــــــــ = ــــــــــ
دهـ م دو م
أب × أ جـ ك ك ك
اذاً : ــــــــــــــــــ = ــــــــــ × ـــــــــ = [ــــــــ]²
دهـ × دو م م م
هذا يكافئ أن فى المثلين المتشابهين النسبة بين
مساحتى المثلثين كالنسبة بين مربع طولى أى ضلعين
متناظرين فيهما .
4 احسب قياس الزاوية x المبينة فى الشكل
الأربعاء، 18 أبريل 2012
التسميات:
حساب مثلثات,
مواضيع متنوعة,
هندسة مستوية
فيه الزاوية O N M = x (بالفرض)
وايضاً : الزاوية O M N = y (بالفرض)
أى أن : x+y = 110
وايضاً فيه المثلث M B C متساوى الساقين :
اذاً : BC = BM
فى المثلث N B C فيه :
BC/sin40 = BN/sin80
اذاً : (1) BC = [BN sin40]/sin80
فى المثلث : M B C فيه :
BM/sinx = BN/sin(y+50) ll
ولكن x+y = 110 ومنها y = 100 - x
اذاً : y + 50 = 160 - x بالتعويض ..
BM/sinx = BN/sin(160 - x) ll
ومنها : BM = [BN sinx]/sin(160 - x) (2
ولكن BC = BM
من (1) ، (2) ينتج أن :
ll [BN sinx]/sin(160 - x) = [BN sin40]/sin80
بإختصار BN من الطرفين ..
ll sinx/sin(160 - x) = sin40/sin80
وهكذا نحصل على (نقبل النسبتين فى الطرفين)
ll sin(160 - x)/sinx = sin80/sin40
الآن قم بنشر sin(160 - x) l بالمتطابقة المعروفة .
ll [sin160 cosx - cos160 sinx]/sinx = sin80/sin40
وبعد توزيع (او قسمة) البسط على المقام نحصل على :
ll sin160 cosx/sinx - cos160 = sin80/sin40
ومنها نحصل على :
ll sin160 cosx/sinx = sin80/sin40 + cos160
بضرب الطرفين فى مقلوب sin160
ll cosx/sinx = sin80/(sin40 sin160) + cos160/sin160
بعد توحيدك للمقامات تحصل على :
ll cosx/sinx = [(sin40 cos160) + sin80] /(sin40 sin160) ll
اذاً :
ll sinx/cosx = (sin40 sin160)/[(sin40 cos160) + sin80] ll
ll tanx = (sin40 sin160)/[(sin40 cos160) + sin80] ll
ومن ثم تستطيع ايجاد معكوس tanx بالآلة الحسابة
او حتى من خلال تبسيط الطرف الأيمن ببعض المتطابقات
المثلثية للوصول الى أن : x = 30ْ
للمزيد من التفاصيل اضغط هنا
0 الدوال الزائدية
الاثنين، 9 أبريل 2012
التسميات:
التفاضل والتكامل,
حساب مثلثات,
مواضيع متنوعة,
هندسة فراغية,
هندسة مستوية
اذا قلنا س² + ص² = 1
تعتبر دائرة الوحدة، والتى تقابلها فى الإحداثيات
البارامترية جتا²س + جا²س = 1
ملحوظة : الأفضل هو وضع رمز غير س للتفرقة
بينه وبين الإحداثيات الكارتيزية،لكن فقط وضعتها
هكذا لأننا تعودنا على شكلها بهذه الصيغة .
ننتقل الى : س² - ص² = 1
هذه أبسط صورة لمعادلة القطع الزائد
والذى فيه :
احداثى الرأس الأيمن : (1 ، 0)
احداثى الرأس الايسر : (-1 ، 0)
فقط اكتفى بهذين الإحداثيين
فإذا رمزنا لجيب التمام الزائدى بالرمز جتازس
والجيب الزائدى بالرمز جازس فيكون :
جتاز²س - جاز²س = 1
وهذه هى المتطابقة الأساسية فى حساب
الدوال الزائدية .
هذه الدوال تتميز بصفات أهمها :
جتاز(0) = 1
جاز(0) = 0
وهذه الخاصية هى نفس الخاصية الموجودة
فى الدوال المثلثية (الدائرية)
ويمكنك استنتاجها من خلال رسم القطع الزائد .
الخاصية الثانية :
مشتقة جتازس تعطى جازس
ومشتقة جازس تعطى جتاس
الإثبات:(لأن هذه الخطوة هامة جداً)
نستطيع ان نثبت إثبات جزئى عندما س=0
(ولكن هذا الأإثبات يتطلب منك رسم كلاً من
دالتى جتازس ، جازس)
فى حين أن هناك إثبات اسهل بكثير وهو :
بما أن : جتاز²س - جاز²س = 1
اذاً : جتاز²س = جاز²س + 1
الآن اشتق الطرفين بالنسبة لـ س
تجد أن : مشتقة جتاز²س = مشتقة (جاز²س + 1)
ولكن مشتقة الواحد = 0
(اى عندما نشتق يكون لا فائدة منه)
اذاً : مشتقة جتاز²س = مشتقة جاز²س
وبإستخدام قوانين الإشتقاق ..
اذاً : 2جتازس × مشتقة جتازس = 2جازس × مشتقة جازس
بمقارنة الطرفين نجد أن :
مشتقة جتازس = جازس
مشتقة جازس = جتازس
نأخذ هذه المعلومات وننتقل الى متسلسلة ماكلورين .
د(س) = جتازس
دَ(س) = جازس
دً(س) = جتازس
.... وهكذا
نعلم أن : جتاز(0) = 1 وان جاز(0) = 0
اذاًً :
جتازس = 1+س²\2!+س^4\4!+.....
بنفس الطريقة نجد أن :
جازس = س+س³\3!+س^5\5!+......
بجمع المعاداتين معاً ينتج :
جتازس+جازس = 1+س+س²\2!+س³\3!+....
ولكن : 1+س+س²\2!+س³\3!+.... = هـ^س
حيث هـ ≈ 2.71828
اذاً : جتازس + جازس = هـ^س
وهذه من أهم المتطابقات :
لاحظ كما أن دالة جاس فردية فإن دالة جازس فردية ايضاً
وكما ان دالة جتاس زوجية فإن دالة جتازس زوجية ايضاً ..
الآن : هـ^س = جتازس + جازس
نحذف س ونضع - س للطرفين ..
هـ^-س = جتاز(-س) + جاز(- س)
هـ^-س = جتازس - جازس
الآن : لدينا متطابقتين :
هـ^س = جتازس + جازس (1)
هـ^-س = جتازس - جازس (2)
........... بجمع (1) ، (2) .............
هـ^س + هـ^-س = 2جتازس
هـ^س + هـ^-س
ومنها : جتازس = ــــــــــــــــــــــــــــ
2
................ بطرح (1) ، (2) .................
هـ^س - هـ^-س = 2جازس
هـ^س - هـ^-س
ومنها : جازس = ــــــــــــــــــــــــــــ
2
الآن نستطيع وبسهولة أن نثبت أن مشتقة احداهما
تعطى الآخر :
جتازس = ½(هـ^س + هـ^-س)
نشتق الطرفين بالنسبة لـ س
(جتازس) َ = ½(هـ^س - هـ^-س)
= جازس
بنفس الطريقة نثبت أن :
(جازس) َ = جتازس
تستطيع بمعرفة ذلك ايجاد مشتقات بقية الدوال .
جازس
مثلاً : ظازس = ــــــــــــــــــــ
جتازس
هـ^س - هـ^-س 2
= ــــــــــــــــــــــــــ × ـــــــــــــــــــــــــــــ
2 هـ^س + هـ^-س
هـ^س - هـ^-س
= ــــــــــــــــــــــــــــــــــــ
هـ^س + هـ^-س
وبتطبيق قاعدة القسمة لإيجاد مشتقة ظازس
(هـ^س + هـ^-س)² - (هـ^س - هـ^-س)²
= ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
(هـ^س + هـ^-س)²
البسط عبارة عن فرق مربعين بعد التبسيط يصبح :
2هـ^س × 2هـ^-س
= ــــــــــــــــــــــــــــــــــــــــ
(هـ^س + هـ^-س)²
2
= [ــــــــــــــــــــــــــــــــــــ]²
(هـ^س + هـ^-س)
1
= ـــــــــــــــ = قاز²س
جتاز²س
وحتى لا نكرر خطوات زائدة بنفس الطريقة نذكر ما يلى :
د/دس جتازس = جازس
د/دس جازس = جتازس
د/دس ظازس = قاز²س
د/دس ظتازس = - قتاز²س
د/دس قازس = - قازس ظازس
د/دس قتازس = - قتازس ظتازس
أضغط هنا للتتعرف على المشتقات العكسية .
نأتى الى بعض التكاملات :
بما ان مشتقة احداهما يعطى الآخر .
(اقصد جازس ، جتازس )
فإن : ∫جتازس دس = جازس + ث
∫جازس دس = جتازس + ث
ننتقل الى الحالة الأهم .. ماذا لو كانت بدلا ً من س
دالة فى س ؟
جاز[د(س)]
∫جتاز[د(س)] دس = ــــــــــــــــــ + ث
دَ(س)
جتاز[د(س)]
∫جاز[د(س)] دس = ــــــــــــــــــــــ+ ث
دَ(س)
يعنى بإختصار اشتق اشتقاق عادى جداً ثم
اقسم على مشتقة الزاوية .
لكن ماذا نصنع فى الإشتقاق ؟؟
الإشتقاق مرحلة عكسية بدلاً من أن نقسم على
مشتقة الزاوية (نضرب فى مشتقة الزاوية)
مثال (للتوضيح فقط)
مشتقة جتاز[د(س)] = دَ(س) جاز[د(س)]
مثال : اوجد مشتقة جتاز(س² - 1)
د/دس جتاز(س² - 1) = 2س جاز(س² - 1)
بمعرفتك بالمعلومات السابقة تستطيع ايجاد بقية
التكاملات الأساسية بنفسك .
الآن نأتى الى أهم جزء وهو علاقة الدوال الزائدية
بالدوال الدائرية (المثلثية)
ربما تعلم صيغة أويلر للدوال المثلثية وهى :
(متطابقتين هامتين)
هـ^(ت س) = جتاس + ت جاس (1)
هـ^(-ت س) = جتاس - ت جاس (2)
حيث ت وحدة تخيلية = جذر(-1)
هـ هو العدد النيبيرى ≈ 2.71828
بجمع (1) ، (2) ينتج لنا :
هـ^(ت س) + هـ^(-ت س) = 2جتاس
هـ^(ت س) + هـ^(-ت س)
جتاس = ـــــــــــــــــــــــــــــــــــــــــــ
2
بطرح (1) ، (2) ينتج لك :
هـ^(ت س) - هـ^(-ت س)
جاس = ـــــــــــــــــــــــــــــــــــــــــــ
2ت
..................................................
نبدء من المتطابقة الأولى :
هـ^(ت س) + هـ^(-ت س)
جتاس = ـــــــــــــــــــــــــــــــــــــــــــ
2
تعلم أن ت×ت = ت² = -1
وبوضع ت س للطرفين ..
هـ^(ت² س) + هـ^(-ت² س)
جتا(ت س) = ـــــــــــــــــــــــــــــــــــــــــــــ
2
هـ^س + هـ^-س
جتا(ت س) = ـــــــــــــــــــــــــــــــــــــ
2
جتا(ت س) = جتازس
نأخذ المتطابقة الثانية :
هـ^(ت س) - هـ^(-ت س)
جاس = ـــــــــــــــــــــــــــــــــــــــــــ
2ت
بضرب الطرفين فى ت ينتج :
هـ^(ت س) - هـ^(-ت س)
ت جاس = ــــــــــــــــــــــــــــــــــــــــــــــ
2
نضع ت س للطرفين ..
هـ^(ت² س) - هـ^(-ت² س)
ت جا(ت س) = ـــــــــــــــــــــــــــــــــــــــــــ
2
هـ^(- س) - هـ^(س)
ت جا(ت س) = ــــــــــــــــــــــــــــــــــ
2
بضرب الطرفين فى -1
هـ^س - هـ^-س
- ت جا(ت س) = ــــــــــــــــــــــــــــــــــــ
2
- ت جا(ت س) = جازس
بإختصار نريد نذكر ما يلى :
جتازس = جتا(ت س)
جازس = - ت جا(ت س)
ظازس = - ت ظاز(ت س)
ظتازس = ت ظتا(ت س)
قازس = قا(ت س)
قتازس = ت قتا(ت س)
وكما أن هناك متطابقات مثلثية فهناك ايضاً متطابقات زائدية :
نذكر منها :
جتاز(س±ص) = جتازس جتازص ± جازس جازص
جاز(س±ص) = جازس جتازص ± جتازس جازص
ظازس ± ظازص
ظاز(س±ص) = ــــــــــــــــــــــــــــــــــــ
1 ± ظازس ظازص
جاز(2س) = 2 جازس جتازس
جتاز(2س) = جتاز²س + جاز²س
= 2جتاز²س - 1 = 2جاز²س + 1
ظاز²س = 1 - قاز²س
ظتاز²س = 1 + قتاز²س
تعتبر دائرة الوحدة، والتى تقابلها فى الإحداثيات
البارامترية جتا²س + جا²س = 1
ملحوظة : الأفضل هو وضع رمز غير س للتفرقة
بينه وبين الإحداثيات الكارتيزية،لكن فقط وضعتها
هكذا لأننا تعودنا على شكلها بهذه الصيغة .
ننتقل الى : س² - ص² = 1
هذه أبسط صورة لمعادلة القطع الزائد
والذى فيه :
احداثى الرأس الأيمن : (1 ، 0)
احداثى الرأس الايسر : (-1 ، 0)
فقط اكتفى بهذين الإحداثيين
فإذا رمزنا لجيب التمام الزائدى بالرمز جتازس
والجيب الزائدى بالرمز جازس فيكون :
جتاز²س - جاز²س = 1
وهذه هى المتطابقة الأساسية فى حساب
الدوال الزائدية .
هذه الدوال تتميز بصفات أهمها :
جتاز(0) = 1
جاز(0) = 0
وهذه الخاصية هى نفس الخاصية الموجودة
فى الدوال المثلثية (الدائرية)
ويمكنك استنتاجها من خلال رسم القطع الزائد .
الخاصية الثانية :
مشتقة جتازس تعطى جازس
ومشتقة جازس تعطى جتاس
الإثبات:(لأن هذه الخطوة هامة جداً)
نستطيع ان نثبت إثبات جزئى عندما س=0
(ولكن هذا الأإثبات يتطلب منك رسم كلاً من
دالتى جتازس ، جازس)
فى حين أن هناك إثبات اسهل بكثير وهو :
بما أن : جتاز²س - جاز²س = 1
اذاً : جتاز²س = جاز²س + 1
الآن اشتق الطرفين بالنسبة لـ س
تجد أن : مشتقة جتاز²س = مشتقة (جاز²س + 1)
ولكن مشتقة الواحد = 0
(اى عندما نشتق يكون لا فائدة منه)
اذاً : مشتقة جتاز²س = مشتقة جاز²س
وبإستخدام قوانين الإشتقاق ..
اذاً : 2جتازس × مشتقة جتازس = 2جازس × مشتقة جازس
بمقارنة الطرفين نجد أن :
مشتقة جتازس = جازس
مشتقة جازس = جتازس
نأخذ هذه المعلومات وننتقل الى متسلسلة ماكلورين .
د(س) = جتازس
دَ(س) = جازس
دً(س) = جتازس
.... وهكذا
نعلم أن : جتاز(0) = 1 وان جاز(0) = 0
اذاًً :
جتازس = 1+س²\2!+س^4\4!+.....
بنفس الطريقة نجد أن :
جازس = س+س³\3!+س^5\5!+......
بجمع المعاداتين معاً ينتج :
جتازس+جازس = 1+س+س²\2!+س³\3!+....
ولكن : 1+س+س²\2!+س³\3!+.... = هـ^س
حيث هـ ≈ 2.71828
اذاً : جتازس + جازس = هـ^س
وهذه من أهم المتطابقات :
لاحظ كما أن دالة جاس فردية فإن دالة جازس فردية ايضاً
وكما ان دالة جتاس زوجية فإن دالة جتازس زوجية ايضاً ..
الآن : هـ^س = جتازس + جازس
نحذف س ونضع - س للطرفين ..
هـ^-س = جتاز(-س) + جاز(- س)
هـ^-س = جتازس - جازس
الآن : لدينا متطابقتين :
هـ^س = جتازس + جازس (1)
هـ^-س = جتازس - جازس (2)
........... بجمع (1) ، (2) .............
هـ^س + هـ^-س = 2جتازس
هـ^س + هـ^-س
ومنها : جتازس = ــــــــــــــــــــــــــــ
2
................ بطرح (1) ، (2) .................
هـ^س - هـ^-س = 2جازس
هـ^س - هـ^-س
ومنها : جازس = ــــــــــــــــــــــــــــ
2
الآن نستطيع وبسهولة أن نثبت أن مشتقة احداهما
تعطى الآخر :
جتازس = ½(هـ^س + هـ^-س)
نشتق الطرفين بالنسبة لـ س
(جتازس) َ = ½(هـ^س - هـ^-س)
= جازس
بنفس الطريقة نثبت أن :
(جازس) َ = جتازس
تستطيع بمعرفة ذلك ايجاد مشتقات بقية الدوال .
جازس
مثلاً : ظازس = ــــــــــــــــــــ
جتازس
هـ^س - هـ^-س 2
= ــــــــــــــــــــــــــ × ـــــــــــــــــــــــــــــ
2 هـ^س + هـ^-س
هـ^س - هـ^-س
= ــــــــــــــــــــــــــــــــــــ
هـ^س + هـ^-س
وبتطبيق قاعدة القسمة لإيجاد مشتقة ظازس
(هـ^س + هـ^-س)² - (هـ^س - هـ^-س)²
= ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
(هـ^س + هـ^-س)²
البسط عبارة عن فرق مربعين بعد التبسيط يصبح :
2هـ^س × 2هـ^-س
= ــــــــــــــــــــــــــــــــــــــــ
(هـ^س + هـ^-س)²
2
= [ــــــــــــــــــــــــــــــــــــ]²
(هـ^س + هـ^-س)
1
= ـــــــــــــــ = قاز²س
جتاز²س
وحتى لا نكرر خطوات زائدة بنفس الطريقة نذكر ما يلى :
د/دس جتازس = جازس
د/دس جازس = جتازس
د/دس ظازس = قاز²س
د/دس ظتازس = - قتاز²س
د/دس قازس = - قازس ظازس
د/دس قتازس = - قتازس ظتازس
أضغط هنا للتتعرف على المشتقات العكسية .
نأتى الى بعض التكاملات :
بما ان مشتقة احداهما يعطى الآخر .
(اقصد جازس ، جتازس )
فإن : ∫جتازس دس = جازس + ث
∫جازس دس = جتازس + ث
ننتقل الى الحالة الأهم .. ماذا لو كانت بدلا ً من س
دالة فى س ؟
جاز[د(س)]
∫جتاز[د(س)] دس = ــــــــــــــــــ + ث
دَ(س)
جتاز[د(س)]
∫جاز[د(س)] دس = ــــــــــــــــــــــ+ ث
دَ(س)
يعنى بإختصار اشتق اشتقاق عادى جداً ثم
اقسم على مشتقة الزاوية .
لكن ماذا نصنع فى الإشتقاق ؟؟
الإشتقاق مرحلة عكسية بدلاً من أن نقسم على
مشتقة الزاوية (نضرب فى مشتقة الزاوية)
مثال (للتوضيح فقط)
مشتقة جتاز[د(س)] = دَ(س) جاز[د(س)]
مثال : اوجد مشتقة جتاز(س² - 1)
د/دس جتاز(س² - 1) = 2س جاز(س² - 1)
بمعرفتك بالمعلومات السابقة تستطيع ايجاد بقية
التكاملات الأساسية بنفسك .
الآن نأتى الى أهم جزء وهو علاقة الدوال الزائدية
بالدوال الدائرية (المثلثية)
ربما تعلم صيغة أويلر للدوال المثلثية وهى :
(متطابقتين هامتين)
هـ^(ت س) = جتاس + ت جاس (1)
هـ^(-ت س) = جتاس - ت جاس (2)
حيث ت وحدة تخيلية = جذر(-1)
هـ هو العدد النيبيرى ≈ 2.71828
بجمع (1) ، (2) ينتج لنا :
هـ^(ت س) + هـ^(-ت س) = 2جتاس
هـ^(ت س) + هـ^(-ت س)
جتاس = ـــــــــــــــــــــــــــــــــــــــــــ
2
بطرح (1) ، (2) ينتج لك :
هـ^(ت س) - هـ^(-ت س)
جاس = ـــــــــــــــــــــــــــــــــــــــــــ
2ت
..................................................
نبدء من المتطابقة الأولى :
هـ^(ت س) + هـ^(-ت س)
جتاس = ـــــــــــــــــــــــــــــــــــــــــــ
2
تعلم أن ت×ت = ت² = -1
وبوضع ت س للطرفين ..
هـ^(ت² س) + هـ^(-ت² س)
جتا(ت س) = ـــــــــــــــــــــــــــــــــــــــــــــ
2
هـ^س + هـ^-س
جتا(ت س) = ـــــــــــــــــــــــــــــــــــــ
2
جتا(ت س) = جتازس
نأخذ المتطابقة الثانية :
هـ^(ت س) - هـ^(-ت س)
جاس = ـــــــــــــــــــــــــــــــــــــــــــ
2ت
بضرب الطرفين فى ت ينتج :
هـ^(ت س) - هـ^(-ت س)
ت جاس = ــــــــــــــــــــــــــــــــــــــــــــــ
2
نضع ت س للطرفين ..
هـ^(ت² س) - هـ^(-ت² س)
ت جا(ت س) = ـــــــــــــــــــــــــــــــــــــــــــ
2
هـ^(- س) - هـ^(س)
ت جا(ت س) = ــــــــــــــــــــــــــــــــــ
2
بضرب الطرفين فى -1
هـ^س - هـ^-س
- ت جا(ت س) = ــــــــــــــــــــــــــــــــــــ
2
- ت جا(ت س) = جازس
بإختصار نريد نذكر ما يلى :
جتازس = جتا(ت س)
جازس = - ت جا(ت س)
ظازس = - ت ظاز(ت س)
ظتازس = ت ظتا(ت س)
قازس = قا(ت س)
قتازس = ت قتا(ت س)
وكما أن هناك متطابقات مثلثية فهناك ايضاً متطابقات زائدية :
نذكر منها :
جتاز(س±ص) = جتازس جتازص ± جازس جازص
جاز(س±ص) = جازس جتازص ± جتازس جازص
ظازس ± ظازص
ظاز(س±ص) = ــــــــــــــــــــــــــــــــــــ
1 ± ظازس ظازص
جاز(2س) = 2 جازس جتازس
جتاز(2س) = جتاز²س + جاز²س
= 2جتاز²س - 1 = 2جاز²س + 1
ظاز²س = 1 - قاز²س
ظتاز²س = 1 + قتاز²س
7 إثبت انه فى اى مثلث أ ب جـ فيه (جاأ+جاب)/جاجـ > 1
الثلاثاء، 27 مارس 2012
التسميات:
الجبر,
مواضيع متنوعة,
هندسة مستوية
حل1: زواياه هى أ ، ب ، جـ نفرض أن أضلاعه أ َ ، بَ ، جـَ
جاأ + جاب أ َ + بَ
ـــــــــــــــــــــــــ = ـــــــــــــــــــــــــ
جاجـ جـَ
يمكن استنتاجها من قانون الجيب : هكذا :
أ َ بَ جـَ
ــــــــــــــ = ــــــــــــــ = ـــــــــــــــــــ
جاأ جاب جاجـ
أ َ جاأ
ومن خواص النسبة والتناسب ينتج أن : ــــــــــــ = ـــــــــــــــ
جـ َ جأجـ
بَ جاب
وايضاً : ــــــــــــ = ــــــــــــــ
جـَ جاجـ
جاأ + جاب أ َ + بَ
اذاً : ـــــــــــــــــــــــ = ـــــــــــــــــــــــــ
جاجـ جـَ
ولكن فى اى مثلث يتحقق فيه أن طول اى ضلعين أكبر من طول الضلع الثالث :
اذاً أ َ + بَ > جـ َ وهذا يدل على أن البسط أكبر من المقام اى أن المقدار
كله حتماً أكبر من الواحد .
.............................................................................................
حل2:
أ+ب+جـ = 180 ومنها أ+ب = 180 - جـ
جاأ + جاب جاأ + جاب
ــــــــــــــــــــــــ = ـــــــــــــــــــــــــــ
جاجـ جا(أ+ب)
وبطرح المقام من البسط اذا نتج انه اقل من الصفر
فهذا دليل على أن المقام اقل من البسط او البسط
اكبر من المقام .. اذاً الكسر كله أكبر من الواحد .
جا(أ+ب) - (جاأ + جاب)
= جاأ جتاب + جتاأ جاب - جاأ - جاب
= جاأ (جتاب - 1) + جاب (جتاأ - 1)
الآن نفرض ان المثلث حاد الزاوية اذاً كلاً من أ ، ب
محصورين فى الفترة ]0 ، 90[
اذاً كلاً من جاأ ، جاب ، جتاأ ، جتاب كميات موجبة
تحصر قيمها فى الفترة ]0 ، 1[
اذاً فى هذه الحالة نتحقق من أن :
جاأ (جتاب - 1) + جاب (جتاأ - 1) < 0
الآن نأخذ الحالة التى يكون فيها المثلث قائم الزاوية
نفرض أن المثلث قائم الزاوية فى جـ فهذا يدل على
أن كلاً من أ ، ب حادتين ويكون بذلك انتهى البرهان
عند هذه الخطوة، ثم نفرض أن المثلث قائم الزاوية
فى أ فيكون بذلك جاأ = 1 و جتاأ = 0 بالتعويض
مع علمان ان ب زاوية حادة فى هذه الحالة .
(جتاب - 1) - جاب < 0
وأخيراً نفرض أن المثلث منفرج الزاوية .
فإذا كان منفرج الزاوية فى جـ هذا يعنى أن كلاً من أ ، ب
حادتين ونكون انتهينا من البرهان، ثم نفرض أن المثلث
منفرج الزاوية فى أ .
هذا يعنى أن كلاً من جاأ ، جاب موجبتين لأن جا موجبة
فى الربع الأول، ولكن جتاأ سالبة لأن جتا سالبة فى الربع الثانى .
فى جميع الحالات يتحقق ايضاً أن :
جاأ (جتاب - 1) + جاب (جتاأ - 1) < 0
وبالمثلث نأخذ حالة ب زاوية منفرجة تتحقق نفس النتيجة
اذاً : جاأ + جاب > جا(أ+ب)
جاأ + جاب
اذاً : ـــــــــــــــــــــــــــ > 1
جا(أ+ب)
جاأ + جاب
ومنها : ـــــــــــــــــــــــــ > 1
جاجـ
وهو المطلوب : إضغط هنا لتتطلع على حل ثالث
جاأ + جاب أ َ + بَ
ـــــــــــــــــــــــــ = ـــــــــــــــــــــــــ
جاجـ جـَ
يمكن استنتاجها من قانون الجيب : هكذا :
أ َ بَ جـَ
ــــــــــــــ = ــــــــــــــ = ـــــــــــــــــــ
جاأ جاب جاجـ
أ َ جاأ
ومن خواص النسبة والتناسب ينتج أن : ــــــــــــ = ـــــــــــــــ
جـ َ جأجـ
بَ جاب
وايضاً : ــــــــــــ = ــــــــــــــ
جـَ جاجـ
جاأ + جاب أ َ + بَ
اذاً : ـــــــــــــــــــــــ = ـــــــــــــــــــــــــ
جاجـ جـَ
ولكن فى اى مثلث يتحقق فيه أن طول اى ضلعين أكبر من طول الضلع الثالث :
اذاً أ َ + بَ > جـ َ وهذا يدل على أن البسط أكبر من المقام اى أن المقدار
كله حتماً أكبر من الواحد .
.............................................................................................
حل2:
أ+ب+جـ = 180 ومنها أ+ب = 180 - جـ
جاأ + جاب جاأ + جاب
ــــــــــــــــــــــــ = ـــــــــــــــــــــــــــ
جاجـ جا(أ+ب)
وبطرح المقام من البسط اذا نتج انه اقل من الصفر
فهذا دليل على أن المقام اقل من البسط او البسط
اكبر من المقام .. اذاً الكسر كله أكبر من الواحد .
جا(أ+ب) - (جاأ + جاب)
= جاأ جتاب + جتاأ جاب - جاأ - جاب
= جاأ (جتاب - 1) + جاب (جتاأ - 1)
الآن نفرض ان المثلث حاد الزاوية اذاً كلاً من أ ، ب
محصورين فى الفترة ]0 ، 90[
اذاً كلاً من جاأ ، جاب ، جتاأ ، جتاب كميات موجبة
تحصر قيمها فى الفترة ]0 ، 1[
اذاً فى هذه الحالة نتحقق من أن :
جاأ (جتاب - 1) + جاب (جتاأ - 1) < 0
الآن نأخذ الحالة التى يكون فيها المثلث قائم الزاوية
نفرض أن المثلث قائم الزاوية فى جـ فهذا يدل على
أن كلاً من أ ، ب حادتين ويكون بذلك انتهى البرهان
عند هذه الخطوة، ثم نفرض أن المثلث قائم الزاوية
فى أ فيكون بذلك جاأ = 1 و جتاأ = 0 بالتعويض
مع علمان ان ب زاوية حادة فى هذه الحالة .
(جتاب - 1) - جاب < 0
وأخيراً نفرض أن المثلث منفرج الزاوية .
فإذا كان منفرج الزاوية فى جـ هذا يعنى أن كلاً من أ ، ب
حادتين ونكون انتهينا من البرهان، ثم نفرض أن المثلث
منفرج الزاوية فى أ .
هذا يعنى أن كلاً من جاأ ، جاب موجبتين لأن جا موجبة
فى الربع الأول، ولكن جتاأ سالبة لأن جتا سالبة فى الربع الثانى .
فى جميع الحالات يتحقق ايضاً أن :
جاأ (جتاب - 1) + جاب (جتاأ - 1) < 0
وبالمثلث نأخذ حالة ب زاوية منفرجة تتحقق نفس النتيجة
اذاً : جاأ + جاب > جا(أ+ب)
جاأ + جاب
اذاً : ـــــــــــــــــــــــــــ > 1
جا(أ+ب)
جاأ + جاب
ومنها : ـــــــــــــــــــــــــ > 1
جاجـ
وهو المطلوب : إضغط هنا لتتطلع على حل ثالث
0 إنشىء شكلاً مناسباً ثم إثبت أن الدالة تآلفية
الأحد، 25 مارس 2012
التسميات:
الجبر,
هندسة مستوية
ABC مثلث بحيث: AB=14 ;BC+12 ;AC=11
نعتبر Mمن القطعة [AB]
المستقيم المار من Mوالموازي للمستقيم (BC) يقطع المستقيم (AC) في النقطة N
نضع AM=x و نعتبر الدالة f بحيث f(x) هو محيط شبه المنحرف MNCB
1) أنشئ شكلا مناسبا
2) بين أن الدالة f دالة تآلفية
أولاً : نرسم شكل تقريبى:
الآن فرضنا أن AM = X ومنها BM = 14 - X
بما أن MN متوازى لـ BC والزاوية Aمشتركة
اذاً المثل ABC يتشابه مه المثلث AMN
,من خواص التشابه يتحقق أن :
AB/AM = BC/MN = AC/AN
ll 14/X = 12/MN = 11/AN
الآن امامنا نسبة كاملة تحتوى على المجهول X
فقط ومن خلالها نوجد MN و AN بدلالة X
ارشاد : استعمل قوانين النسبة والتناسب
كما ان حاصل ضرب الطرفين = حاصل ضرب الوسطين
لتصل الى أن :
MN = 6X/7 و AN = 11X/14
الآن اضبح من السهل جداً التعرف على أضلاع شبه
المنحرف بدلالة X وهى :
MN = 6X/7 و BC = 12
BM = 14 - X و NC = 11 - AN
NC = 11 - 11X/14
f(x) = 6X/7 + 12 + 14 - X + 11 - 11X/14
f(x) = 6X/7 - 11X/14 - X + 37
وحد المقامات بالنسبة لـ X
f(x) = -13x/14 + 37
الدالة تآلفية وميلها = -13 على 14
0 ما نوع المثلث الذى يتحقق فيه cosA+cosB+cosC=3\2 ؟
الثلاثاء، 20 مارس 2012
التسميات:
حساب مثلثات,
مواضيع متنوعة,
هندسة مستوية
هناك عدة طرق يمكن ان نتحقق من خلالها على نوعية
المثلث .. أذكر منها قانون جيب التمام، وبتحويل كلاً منcosA و cosB و cosC فنحصل على الآتى :
ll (a²+b²-c²)/2ab +(a²+c²-b²)/2ac + (b²+c²-a²)/2bc =3/2
بضرب الطرفين فى 2abc
ll c(a²+b²-c²) + b(a²+c²-b²) + a(b²+c²-a²) =3abc
ومنها نحصل على :-
ll c(a²+b²) + b(a²+c²) + a(b²+c²) =a³+b³+c³+3abc
ca²+cb² + ba²+bc² + ab²+ac² = a³+b³+c³+3abc
بحذف 6abc من الطرفين فنحصل على :
مع توزيعها على الطرف الأيسر هكذا ...
ca²+cb²-2abc + ba²+bc²-2abc + ab²+ac²-abc = a³+b³+c³-3abc
بإكمال المربعات فى الطرف الأيسر مع أخذ العوامل المشتركة ..
c(a-b)²+b(a-c)²+a(b-c)² = a³+b³+c³-3abc
استطيع ان اثبت لك أن :
a³+b³+c³-3abc = (a+b+c)(a²+b²+c² - ab - bc - ac) ll
من خلال ذلك نتحقق من أن : -
c(a-b)²+b(a-c)²+a(b-c)² = (a+b+c)(a²+b²+c² - ab - bc - ac) ..ll
بضرب الطرفين فى 2 ومن ثم نقوم بأكمال المربعات
فى الطرف الأيمن ( كما فعلنا فى الطرف الأيسر )
فنحصل فى النهاية على :-
ll 2c(a-b)²+2b(a-c)²+2a(b-c)² = (a+b+c)[(a-b)²+(a-c)²+(b-c)²] ll
الآن اطرح عناصر الطرف الأيمن من الأيسر (اى اجعل المعادلة صفرية)
مع اجراء بعض العمليات الجبرية واخذ العواملة المشتركة فنحصل على :
ll (a - b - c) ( b - c )² + (b -a - c) ( c - a )² + ( c- a - b) ( a - b )² = 0 ll
ربما تعلم أنه فى اى مثلث فإن مجموع اى ضلعين فيه أكبر من طول الضلع الثالث
وهذا يعنى ان مصدر الصفر فى المعادلة مستحيل يكون من الأقواس التى تتشابه
مع (a - b - c) كمثال يعنى .
اذاً مصدر الصفر من الأقواس الثنائية الأخرى ( التربيعية )
وهذا يعنى أن :
b - c = 0 ومنها b = c
c - a = 0 ومنها c = a
وهذا يكفى ( علاقة تعدى ) نستنتج منها أن :
a = b = c
اذاً المثلث (متساوى الأضلاع)
............................................................................
حل آخر عن طريقة دلتا ( المميز ) فى المعادلة التربيعية
عن طريق التطبيق المباشر للمتطابقة المثلثية :
cosA+cosB = 2cos½(A+B) cos½(A-B) ..ll
والمتطابقة : cos2x = 1 - 2sin²x
ومنها نحصل على أن : cosC = 1 - 2sin²(C/2) ..ll
كذلك تذكر متطابقة دوال الجيب وجيب التمام المتممة :
cos(90 - x) = sinx
وايضاً تذكر أن مجموع زوايا المثلث = 180 درجة
A+B+C = 180
A+B = 180 - C
........ إعتبر الذى فات كله مقدمة ........
الآن : cosA+cosB+cosC=3\2
2cos½(A+B) cos½(A-B) + cosC = 3/2
بضرب الطرفين فى 2
4cos½(A+B) cos½(A-B) + cosC = 3
4cos½(180 - C) cos½(A-B) +2cosC = 3
4cos(90 - C/2) cos½(A-B) +2(1 - 2sin²(C/2)) = 3
4sin(C/2) cos½(A-B) +2 - 4sin²(C/2) = 3
4sin(C/2) cos½(A-B) +2 - 4sin²(C/2) -3 = 0
4sin(C/2) cos½(A-B) - 4sin²(C/2) - 1 = 0
بترتيب الحدود مع ضرب الطرفين فى -1
4sin²(C/2) - 4cos½(A-B) sin(C/2) + 1 = 0
نعتبر انها معادلة تربيعية فى sin(C/2) ..ll
وبإيجاد مميز المعادلة، وبما اننا نريد الحلول الحقيقية
فقط اذاً ما تحت الجذر التربيعى أكبر من او يساوى الصفر .
ll 16cos²½(A-B) - 4×4×1 ≥ 0
بقسمة الطرفين على 16
cos²½(A-B) - 1 ≥ 0
cos²½(A-B) ≥ 1
بأخذ الجذر التربيعى للطرفين
cos½(A-B) ≥ ±1
cos(½A - ½B) ≥ ±1
لكن انت تعلم ان مدى دالة cos محصور فى الفترة [-1 , 1]
اذاً نأخذ حالة المساواه فقط : cos(½A - ½B) = ±1
اذاً ما داخل الزاوية cos = معكوس جيب التمام لـ 1 وهو 0
والحالة الثانية (سالب واحد ) نجد ان المعكوس هو 180
بالقياس السيتنى ..
اذاً : ll ½A - ½B = 0
ومنها A - B = 0 ومنها A = B
او ll ½A - ½B = 180 بضرب الطرفين فى 2
A - B = 360 ولكن هذا مستحيل ان يحدث فى أى مثلث
لأن مجموع زوايا المثلث = 180
اذاً نأخذ الحالة الأولى فقط وهى أن A = B
بنفس الطريقة نصنع نفس الخطوات :
cosA+cosB+cosC=3\2
ولكن هذه المرة نطبق المتطابقة على cosB+cosC
لينتج لنا أن B = C
وتلاحظ انها علاقة تعدى وينتج منها أن A=B=C
اذاً المثلث متساوى الأضلاع .
................................................................
حل ثالث : بحيث يمكن وضع A=B=C = 60
تجدها تحقق المعادلة، والآن نريد أن نثبت وحدانيتها .
cosA+cosB+cosC=3\2
ولكن C = 180 - (A+B) ..ll
اذاً : cosC = - cos(A+B) ...ll
ومنها ينتج أن : cosA+cosB - cos(A+B)=3\2
الآن نفرض دالة فى A , b بحيث :
f(A,B) = cosA+cosB - cos(A+B) ..ll
اوجد المشتقة الجزئية بالنسبة لـ A
ثم اوجد المشتقة الجزئية بالنسبة لـ B
ومن ثم مساواة كلاً منهم بالصفر وحلهم
معاً ينتج لنا النقاط الحرجة للدالة .
f'A = sinA + sin(A+B) ..ll
f'B = -sin(B) + sin(A+B) ..ll
f'A = f'B = 0 ومنها نحصل على ان :
sinA = sinB = sin(A+B) ...ll
نأخذ أولاً الحالة sinA = sinB فنحصل منها على
A=B أو A = 180 - B وهذا الحل مرفوض لأنه اذا تحقق
يكون A+B = 180 مما يعنى ان الشكل ليس مثلثاً أصلاً
لأن مجموع زوايا المثلث A+B+C = 0 فلا يمكن ان تكون
زاوية منهم بصفر .
ثم نأخذ الحالة الثانية مع الآخذ فى الإعتبار أن A=B
sinA = sin(A+B) = sin2A
فنحصل على انه اما A = 2A ومنها 1 = 2 مرفوض او A = 0
مرفوض ايضاً .
واما A = 180 - 2A ((طبعاً لأن sin موجبة فى الربع الثانى))
ومنها 3A = 180 اذاً A = 60
مما سبق نتأكد من أنه A=b = 60 نقطة حرجة للدالة
ينتج من خلالها أن A=B=C نقطة حرجة للدالة مما يعنى
او تساوى 3/pi بالقدير الدائرى .
الآن ندرس ما اذا كانت قيمة عظمى ام صغرى محلية
بحيث اذا كانت المشتقة الجزئية الثانية بالنسبة لـ A
عندما A = B = pi/3 أقل من الصفر ، وكان الشرط
f'aa . fbb - f'ab² < 0 كانت قيمة عظمى محلية
f'aa = -cos(a) + cos(a+b) ...ll
f'bb = -cos(b) + cos(a+b) ...ll
f'ab = cos(a+b) ...ll
f_aa(pi/3 , pi/3) = -1 < 0
f'aa . fbb - f'ab² = 3/4 > 0
اذاً النقطة (pi/3 , pi/3) قيمة عظمى محلية .
فى المجال : ll (0,pi) × (0,pi) ..ll
الآن نختبر هل هى قيمة عظمى مطلقة ؟
بحيث نقارنها بنقاط حواف الدالة والنقط الركنية لها .
بحيث تكون النقاط هى :
ll (0 , B) ..ll B from 0 to pi
ll (A , 0) ll A from 0 to pi
ll (pi ,B) ll B from 0 to pi
ll (A , pi) ll A from 0 to pi
أولاً نجرب النقاط الركنية ومنها النقطة (0 ، 0)
فى الدالة : f(A,B) = cosA+cosB - cos(A+B) ..ll
f(0,0) = f(0,pi) = f(pi,0) = 1
f(pi , pi) = -3
f(0,B) = f(A,0) 1 من اجل ,b , A فى الفترة (0 ، pi)
f(pi,B) = 2cosB - 1 ≤ 1 من أجل B فى الفترة (0 ، pi)
f(ِِA,pi) = 2cosA - 1 ≤ 1 من أجل A فى الفترة (0 ، pi)
فى حين أننا اذا ما عوضنا بالنقطة الحرجة (pi/3 , pi/3)
f (pi/3 , pi/3) = 3/2
اذاً (pi/3 , pi/3) قيمة عظمى مطلقة للدالة فى
المجال ll (0,pi) × (0,pi) ..ll
اذاً : cosA+cosB+cosC=3\2
اذا واذا فقط A=B=C = pi/3
او 60 درجة بالقياس الستينى .
اذاً المثلث متساوى الأضلاع .
0 اوجد معادلة الدائرة التى تمس محور السينات فى النقطة (-2 ، 0) وتقطع جزءاً من محور الصادات طوله 4جذر(3)
الخميس، 15 مارس 2012
التسميات:
هندسة تحليلية,
هندسة مستوية
الصورة العامة لمعادلة الدائرة التى مركزها (د ، هـ)
ونصف قطرها نق هى : -
(س - د)² + (ص - هـ)² = نق²
وبما انها تمس محور السينات فى النقطة التى ذكرتها
اذاً د = -2 ، هـ = نق
((تستطيع ايضاً ان توجدها عن طريق المشقتة الأولى
لكنها تعتبر خطوات زائدة ))
.........................................................
وتقطع من محور الصادات الموجب وترا طوله 4جذر(3)
تعلم ان نصف القطر عمودى على الوتر وينصفه
اذاً ينصبفه الى 2جذر(3) ، 2جذر(3)
ومن ثم يكون طول الضلع الأفقى (كما هو مبين بالرسم)
يساوى 2 ( لأنه موازى لمحور السينات من -2 الى 0 )
وطبعاً لا يوجد طول ضلع بالسالب لذلك نقول ان الطول
= |-2| = 2
الآن الوتر فى المثلث القائم هو (نق) = هـ
استخدم نظرية فيثاغورث :
هـ² = (2)² + (2جذر3)²
هـ² = 16 ومنها هـ = 4 ، نق = 4
الآن : د = -2 ، هـ = 4 ، نق = 4
اذاً : معادلة الدائرة اصبحت :
(س + 2)² + (ص - 4)² = 16
ونصف قطرها نق هى : -
(س - د)² + (ص - هـ)² = نق²
وبما انها تمس محور السينات فى النقطة التى ذكرتها
اذاً د = -2 ، هـ = نق
((تستطيع ايضاً ان توجدها عن طريق المشقتة الأولى
لكنها تعتبر خطوات زائدة ))
.........................................................
وتقطع من محور الصادات الموجب وترا طوله 4جذر(3)
تعلم ان نصف القطر عمودى على الوتر وينصفه
اذاً ينصبفه الى 2جذر(3) ، 2جذر(3)
ومن ثم يكون طول الضلع الأفقى (كما هو مبين بالرسم)
يساوى 2 ( لأنه موازى لمحور السينات من -2 الى 0 )
وطبعاً لا يوجد طول ضلع بالسالب لذلك نقول ان الطول
= |-2| = 2
الآن الوتر فى المثلث القائم هو (نق) = هـ
استخدم نظرية فيثاغورث :
هـ² = (2)² + (2جذر3)²
هـ² = 16 ومنها هـ = 4 ، نق = 4
الآن : د = -2 ، هـ = 4 ، نق = 4
اذاً : معادلة الدائرة اصبحت :
(س + 2)² + (ص - 4)² = 16
1 ادرس الشكل الذى فيه النقط (A(-2,3 و (B(2,1 و (C(-5,-1 و النقطة D بحيث المتجهة CD تساوي 2 * المتجهة AB
الجمعة، 2 مارس 2012
التسميات:
الجبر,
هندسة تحليلية,
هندسة مستوية
نعتبر النقط (A(-2,3 و (B(2,1 و (C(-5,-1 و النقطة D بحيث المتجهة CD تساوي 2 * المتجهة AB
لتكن النقطتين I و J منتصفي القطعتين [AB] و [CD]
على التوالي
1/ أ - ما هي طبيعة الرباعي ABCD مع التعليل
1/ب- حدد زوج احداثياث كل من النقط D و I و J
2/ المستقيم (AC) يقطع المستقيم (BD) في النقطة E
أ - حدد معادلة ديكارتية للمستقيم (AC) و تمثيلا بارمتريا (BD)
ب- استنتج زوج احداثيات النقطة E
ج- بين أن النقطة E تنتمي الى المستقيم (IJ)
3/ المستقيم (AD) يقطع المستقيم (BC) في النقطة F
أ- حدد زوج احداثياث النقطة F
ب- بين أن النقط E و F و I و J مستقيمية
4/انشــــاء الشكــــل كامـــــــلا www.
لتكن النقطتين I و J منتصفي القطعتين [AB] و [CD]
على التوالي
1/ أ - ما هي طبيعة الرباعي ABCD مع التعليل
1/ب- حدد زوج احداثياث كل من النقط D و I و J
2/ المستقيم (AC) يقطع المستقيم (BD) في النقطة E
أ - حدد معادلة ديكارتية للمستقيم (AC) و تمثيلا بارمتريا (BD)
ب- استنتج زوج احداثيات النقطة E
ج- بين أن النقطة E تنتمي الى المستقيم (IJ)
3/ المستقيم (AD) يقطع المستقيم (BC) في النقطة F
أ- حدد زوج احداثياث النقطة F
ب- بين أن النقط E و F و I و J مستقيمية
4/انشــــاء الشكــــل كامـــــــلا www.
هذا اضرب نموذج للشكل الذى يعنيه السؤال ( فى المراجع )
1/ أ - ما هي طبيعة الرباعي ABCD مع التعليل
1/ب- حدد زوج احداثياث كل من النقط D و I و J
................................................................
كما يظهر واضحاً فى الشكل انه شبه منحرف، والتعليل
كما يلى، لكى نقارن بين متجه ومتجه آخر فى المستوى
من حيث الطول يجب ان يكونوا متوازيين ( لأنهم يعبروا عن اتجاه )
ولكن هناك قاعدة اكبر من قاعدة أخرى .. اذاً طبيعة الشكل هو شبه
منحرف ( غير متساوى الساقين ) كما سنبين لاحقاً .
لكى نحددد زوج الإحداثيات للنقطة D نستعين بالمعطى :
المتجهة CD تساوي 2 * المتجهة AB
المتجهة CD = نهايته - بدايته
نفرض ان D هى النطقة (x , y) بحيث ان المتجه CD
= (x+5 , y+1)
ايضاً ضعف المتجه AB = 2(4 , -2) = (8,-4) ll
الآن المتجهة CD تساوي 2 * المتجهة AB
(x+5 , y+1) = (8,-4)
x+5 = 8 ومنها x = 3
y+1 = -4 ومنها y = -5
اذاً احداثى النقطة D (-3 , 5) ..l
.................................................
الآن لاحظ ان كلاً من احداثيات J , I هى عبارة
عن منصفات قطعة مستقيمة ، وطبع قانون المنصف
بأن تجمع الإراتيب وتقسم على 2 ، والأفاصيل وتقسم على 2
I = ((2-2)/2 , (3+1)/2) = (0 , 2) ...l
j = ((-5+3)/2 , (-1-5)/2) = (-1 , -3) ..l
░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░
2/ المستقيم (AC) يقطع المستقيم (BD) في النقطة E
أ - حدد معادلة ديكارتية للمستقيم (AC) و تمثيلا بارمتريا (BD)
ب- استنتج زوج احداثيات النقطة E
ج- بين أن النقطة E تنتمي الى المستقيم (IJ)
نفرض ان معادلة AC هى المستقيم y = mx+a
ولكن المستقيم AC يحقق النقتطين A(-2,3) , C(-5,-1) ..l
m = (3--1)/-2--5) = 4/3
y = 4/3x + a
عوض بأى نقطة ولتكن A
3 = -8/3 + a ومنها a = 17/3
اى ان معادلة الخط المستقيم AC هى y = 4/3x + 17/3
........................................................................
تمثيلا بارمتريا (BD) :
نضع المستقيم BD على الصورة y = mx + a
m = (1--5)/2-3) = 6/-1 = -6
y = -6x + a
عوض بالنقطة B(2,1) ..l
1 = -12 + a ومنها a = 13
y = -6x + 13
let y = t
t = -6x + 13
6x = 13 - t
x = 13/6 - t/6
...................................................................
ب- استنتج زوج احداثيات النقطة E
بالنظر الى الشكل تجد ان E تتقاطع خارج الشكل الرباعى
وايجادها يكون بحل المستقيمين AC و BD
AC : y = 4/3x + 17/3
BD : y = -6x + 13
4/3x + 17/3 = -6x + 13
4/3x + 6x = 13 - 17/3
22/3x = 22/3 بقسمة الطرفين على 22/3
x = 1
الآن عوض فى اى معادلة لإيجاد الإحداثى y
y = -6x + 13
y = -6 + 13 = 7
اذا احداثيات E هى E (1 ; 7) ..l
..............................................................
ج- بين أن النقطة E تنتمي الى المستقيم (IJ)
الحل : نوجد المستقيم Ij بحيث نضعه على الصورة
الديكارتية y = xm+a
بحيث يمر هذا المستقيم بالنقط I (0 , 2) , j(-1 , -3) .l
m = (2--3)/(0--1) = 5
y = 5x + a
عوض بأى نقطة منهم ولتكن I (0 , 2) .l
2 = 0 + a ومنها a = 2
اى ان معادلة المستقيم Ij هى y = 5x + 2
الآن عوض بالنقطة E (1 ; 7) ..l اذا حققت المعادلة
فهى بالفعل تنتمى للمستقيم Ij
y = 5x + 2
7 = 5 + 2
بالفعل تحققها لأن 7 = 5 + 2 = 7
اذاً النقطة E تنتمي الى المستقيم (IJ)
░░░░░░░░░░░░░░░░░░░░░░░░░░░░
3/ المستقيم (AD) يقطع المستقيم (BC) في النقطة F
أ- حدد زوج احداثياث النقطة F
ب- بين أن النقط E و F و I و J مستقيمية
الحل : اذا اردنا ايجاد احداثيات النقطة F فإننا نحل
المستقيمين AD و BC معاً بأى طريقة وتستطيع
حلهم بواسطة المصفوفات .
AD يمر بالنقطتين A(-2 , 3 ) , D(3 , -5) ..l
AD : y = mx+a
m = (3--5)/-2-3) = -8/5
y = -8/5x + a
عوض بالنقطة A(-2 , 3 ) ,,l
3 = 16/5 + a ومنها a = -1/5
AD : y = -8/5x-1/5
بنفس الطريقة نوجد معادلة المستقيم BC
الذى يمر بالنقطيتين B(2 , 1) , C(-5 , -1) ..l
BC : y = mx+a
m = (1--1)/2--5) = 2/7
y = 2/7 x + a
عوض بالنقطة B(2 , 1) ..l
1 = 4/7 + a ومنها a = 3/7
BC : y = 2/7x+3/7
الآن نضع :
AD : y = -8/5x-1/5
BC : y = 2/7x+3/7
2/7x+3/7 = -8/5x-1/5
2/7x + 8/5x = -3/7 - 1/5
66/35x = - 22/35 بضرب الطرفين فى 35
66x =- 22
x = -22/66
x = - 1/3
بالتعويض فى اى معادلة لإيجاد الإحداثى y .
BC : y = 2/7x+3/7
y = 2/7 * -1/3 + 3/7
y = 1/3
اذاً احداثى النقطة F هو F(-1/3 , 1/3) ..l
.........................................................
ب- بين أن النقط E و F و I و J مستقيمية
الآن النقطة F تنتمى للمستقيم IJ فى حالة واحدة فقط
اذا كانت تحقق المستقيم هذا المستقيم ..
y = 5x + 2 هذا معادلة IJ
عوض بالنقطة F(-1/3 , 1/3) ..l
لكى نتحقق من ان :
1/3 = -1/3 .5 + 2
بالفعل المعادلة صحيحة تماماً والنقطة F تحقق
المستقيم IJ
ولكننا اثبتنا فى المطلوب الثانى ان النقطة E ايضاً
تنتمى للمستقيم Ij .
اذاً النقط E و F و I و J مستقيمية .
░░░░░░░░░░░░░░░░░░░░░░░░░░
4/انشــــاء الشكــــل كامـــــــلا
بالفعل تم انشاء الشكل بالكامل كما فى المراجع .
وهو عبارة عن الشكل E C D .
1/ أ - ما هي طبيعة الرباعي ABCD مع التعليل
1/ب- حدد زوج احداثياث كل من النقط D و I و J
................................................................
كما يظهر واضحاً فى الشكل انه شبه منحرف، والتعليل
كما يلى، لكى نقارن بين متجه ومتجه آخر فى المستوى
من حيث الطول يجب ان يكونوا متوازيين ( لأنهم يعبروا عن اتجاه )
ولكن هناك قاعدة اكبر من قاعدة أخرى .. اذاً طبيعة الشكل هو شبه
منحرف ( غير متساوى الساقين ) كما سنبين لاحقاً .
لكى نحددد زوج الإحداثيات للنقطة D نستعين بالمعطى :
المتجهة CD تساوي 2 * المتجهة AB
المتجهة CD = نهايته - بدايته
نفرض ان D هى النطقة (x , y) بحيث ان المتجه CD
= (x+5 , y+1)
ايضاً ضعف المتجه AB = 2(4 , -2) = (8,-4) ll
الآن المتجهة CD تساوي 2 * المتجهة AB
(x+5 , y+1) = (8,-4)
x+5 = 8 ومنها x = 3
y+1 = -4 ومنها y = -5
اذاً احداثى النقطة D (-3 , 5) ..l
.................................................
الآن لاحظ ان كلاً من احداثيات J , I هى عبارة
عن منصفات قطعة مستقيمة ، وطبع قانون المنصف
بأن تجمع الإراتيب وتقسم على 2 ، والأفاصيل وتقسم على 2
I = ((2-2)/2 , (3+1)/2) = (0 , 2) ...l
j = ((-5+3)/2 , (-1-5)/2) = (-1 , -3) ..l
░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░
2/ المستقيم (AC) يقطع المستقيم (BD) في النقطة E
أ - حدد معادلة ديكارتية للمستقيم (AC) و تمثيلا بارمتريا (BD)
ب- استنتج زوج احداثيات النقطة E
ج- بين أن النقطة E تنتمي الى المستقيم (IJ)
نفرض ان معادلة AC هى المستقيم y = mx+a
ولكن المستقيم AC يحقق النقتطين A(-2,3) , C(-5,-1) ..l
m = (3--1)/-2--5) = 4/3
y = 4/3x + a
عوض بأى نقطة ولتكن A
3 = -8/3 + a ومنها a = 17/3
اى ان معادلة الخط المستقيم AC هى y = 4/3x + 17/3
........................................................................
تمثيلا بارمتريا (BD) :
نضع المستقيم BD على الصورة y = mx + a
m = (1--5)/2-3) = 6/-1 = -6
y = -6x + a
عوض بالنقطة B(2,1) ..l
1 = -12 + a ومنها a = 13
y = -6x + 13
let y = t
t = -6x + 13
6x = 13 - t
x = 13/6 - t/6
...................................................................
ب- استنتج زوج احداثيات النقطة E
بالنظر الى الشكل تجد ان E تتقاطع خارج الشكل الرباعى
وايجادها يكون بحل المستقيمين AC و BD
AC : y = 4/3x + 17/3
BD : y = -6x + 13
4/3x + 17/3 = -6x + 13
4/3x + 6x = 13 - 17/3
22/3x = 22/3 بقسمة الطرفين على 22/3
x = 1
الآن عوض فى اى معادلة لإيجاد الإحداثى y
y = -6x + 13
y = -6 + 13 = 7
اذا احداثيات E هى E (1 ; 7) ..l
..............................................................
ج- بين أن النقطة E تنتمي الى المستقيم (IJ)
الحل : نوجد المستقيم Ij بحيث نضعه على الصورة
الديكارتية y = xm+a
بحيث يمر هذا المستقيم بالنقط I (0 , 2) , j(-1 , -3) .l
m = (2--3)/(0--1) = 5
y = 5x + a
عوض بأى نقطة منهم ولتكن I (0 , 2) .l
2 = 0 + a ومنها a = 2
اى ان معادلة المستقيم Ij هى y = 5x + 2
الآن عوض بالنقطة E (1 ; 7) ..l اذا حققت المعادلة
فهى بالفعل تنتمى للمستقيم Ij
y = 5x + 2
7 = 5 + 2
بالفعل تحققها لأن 7 = 5 + 2 = 7
اذاً النقطة E تنتمي الى المستقيم (IJ)
░░░░░░░░░░░░░░░░░░░░░░░░░░░░
3/ المستقيم (AD) يقطع المستقيم (BC) في النقطة F
أ- حدد زوج احداثياث النقطة F
ب- بين أن النقط E و F و I و J مستقيمية
الحل : اذا اردنا ايجاد احداثيات النقطة F فإننا نحل
المستقيمين AD و BC معاً بأى طريقة وتستطيع
حلهم بواسطة المصفوفات .
AD يمر بالنقطتين A(-2 , 3 ) , D(3 , -5) ..l
AD : y = mx+a
m = (3--5)/-2-3) = -8/5
y = -8/5x + a
عوض بالنقطة A(-2 , 3 ) ,,l
3 = 16/5 + a ومنها a = -1/5
AD : y = -8/5x-1/5
بنفس الطريقة نوجد معادلة المستقيم BC
الذى يمر بالنقطيتين B(2 , 1) , C(-5 , -1) ..l
BC : y = mx+a
m = (1--1)/2--5) = 2/7
y = 2/7 x + a
عوض بالنقطة B(2 , 1) ..l
1 = 4/7 + a ومنها a = 3/7
BC : y = 2/7x+3/7
الآن نضع :
AD : y = -8/5x-1/5
BC : y = 2/7x+3/7
2/7x+3/7 = -8/5x-1/5
2/7x + 8/5x = -3/7 - 1/5
66/35x = - 22/35 بضرب الطرفين فى 35
66x =- 22
x = -22/66
x = - 1/3
بالتعويض فى اى معادلة لإيجاد الإحداثى y .
BC : y = 2/7x+3/7
y = 2/7 * -1/3 + 3/7
y = 1/3
اذاً احداثى النقطة F هو F(-1/3 , 1/3) ..l
.........................................................
ب- بين أن النقط E و F و I و J مستقيمية
الآن النقطة F تنتمى للمستقيم IJ فى حالة واحدة فقط
اذا كانت تحقق المستقيم هذا المستقيم ..
y = 5x + 2 هذا معادلة IJ
عوض بالنقطة F(-1/3 , 1/3) ..l
لكى نتحقق من ان :
1/3 = -1/3 .5 + 2
بالفعل المعادلة صحيحة تماماً والنقطة F تحقق
المستقيم IJ
ولكننا اثبتنا فى المطلوب الثانى ان النقطة E ايضاً
تنتمى للمستقيم Ij .
اذاً النقط E و F و I و J مستقيمية .
░░░░░░░░░░░░░░░░░░░░░░░░░░
4/انشــــاء الشكــــل كامـــــــلا
بالفعل تم انشاء الشكل بالكامل كما فى المراجع .
وهو عبارة عن الشكل E C D .
