اوجد مساحة شبه المنحرف المبين بالرسم
الخميس، 17 نوفمبر 2011
التسميات:
حساب مثلثات,
هندسة مستوية
أ ب جـ د شبه منحرف متساوى
الساقين، أ ب يوازى دجـ ، لتكن و نقطة تقاطع قطريه بحيث
تحقق العلاقة وأ / وجـ = 1\3 (( هذه الخطوة للتصحيح ))
فإذا علمت ان مساحة المثلث ب و جـ = 15 فإن مساحة
شبه المنحرف أ ب جـ د = ؟؟
الحل : تعريفات لن اذكرها .. جاو = جا الزاوية المكملة لها
مساحة المثلث = ½ حاصل ضرب طول اى ضلعين فى جيب
الزاوية المحصورة بينهم .. ، نظرية هامة فى الهندسة المستوية
اذا رسما مثلثان على قاعدة وفى جهة واحدة منها ، ينحصران
بين مستقيمين متوازيين، كانا متساويان فى المساحة ( على ما اذكر )
اذاً : مساحة المثلث أ د جـ = مساحة المثلث ب د جـ
ولكن المثلث و د جـ ( مشترك بينهم ) اذاً مساحة المثلث
أ و د = مساحة المثلث ب و جـ = 15
وايضاً هناك تشابه بين المثلثين و أ ب ، و د جـ حيث يحقق
ان ( خطوة لن اذكرها وهى عبارة نسب بين اطوال اضلاع )
نستنتج منها ما هو موضح بالرسم ..
نأتى الى المثلث الذى مساحته 15 وحدة مربعة
حيث نستنتج منه الآتى : ½ 3 م² جاو = 15
اذاً : م² جاو = 10 ومنها :
10
جاو = ــــــــــــــ
م²
الآن وبكل بساطة نستطيع ايجاد مساحة كلاً من المثلثين و د جـ ، و أ ب
اولاً مساحة المثلث و أ ب = ½ م² جاو بالتعويض عن جاو
10
مساحة المثلث = ½ م² × ـــــــــــــ = 5 وحدات مربعة
م²
10
مساحة المثلث و د جـ = ½ 9 م² × ــــــــــــــ = 45 وحدة مربعة
م²
اذاً مساحة شبه المنحرف أ ب جـ د = (2×15) + 45 + 5 = 80 وحدة مربعة


































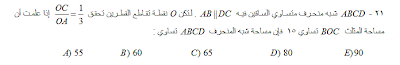








0 التعليقات:
إرسال تعليق