كيفية ايجاد مساحة الدائرة الداخلة للمثلث ؟

لدينا في المثلث نقطة تقاطع المنصفات هي مركز الدائرة التي داخل المثلث
السؤال هو كيف نحسب مساحة هذه الدائرة؟ هل يوجد قانون اوشيء ما يساعد في حساب مساحتها؟
علما ان نصف قطرها مجهول، والمعلوم هو اطوال المثلث .

لك فقط ان تعلم قاعدة هيرون لإيجاد مساحة
المثلث بدلالة أطوال أضلاعه، فإذا كانت أطوال أضلاع المثلث (اى مثلث)
هى a , b , c  فإن مساحته هى : A = sqrt[s(s-a)(s-b)(s-c)]  l
حيث s = (a+b+b)/2  أو بإختصار s هى نصف محيط المثلث، .
(اثبات مفصل لقاعدة هيرون)

ننتقل الآن الى سؤالنا : فكما أنك قلت ان الدائرة الداخلة للمثلث مركزها هو
نقطة تلاقى منصفات هذا المثلث، فإنه ايضاً من الضرورى ان تعلم ان نفس هذه
النقطة (مركز الدائرة) هى نقطة تلاقة انصاف أقطار الدائرة (حقيقة)، ومن ضمن
هذه الأنصاف اقطار التى تكون عمودى على المماس (المماسات هنا أضلاع المثلث)

نظرية : نصف القطر عمود على المماس .

فكرة الحل بسيطة جداً وهى ننا لو علمنا نصف قطر الدائرة لأوجدنا مساحتها .
الآن نعلم ان مساحة المثلث (بقاعدة هيرون) هى :
                                    A = sqrt[s(s-a)(s-b)(s-c)]  l

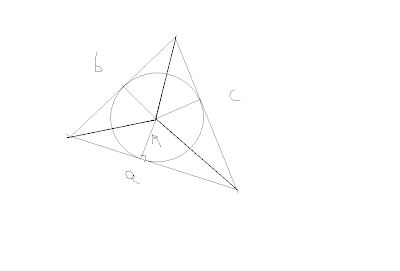
ولكن يمكن ايجاد مساحة المثلث بطريقة أخرى (او كام  هو موضح بالرسم)

مساحة المثلث = مساحة ثلاث مثلثات جميع ارتفاعتها (نصف قطر الدائرة)

مساحة المثلث = ½ القاعدة × الإرتفاع .

والآن بعد تقسيم المثلث (المحيط بالدائرة) الى ثلاث مثلثات نستطيع ان نوجد A
بطريقة أخرى وهى :

A = ½ar + ½br + ½cr = r(a+b+c)/2 = rs

اذاً : rs =  sqrt[s(s-a)(s-b)(s-c)]  l  بتربيع الطرفين ..

r²s² = s(s-a)(s-b)(s-c)  l   بقسمة الطرفين على s²

r² = (s-a)(s-b)(s-c)/s    بضرب الطرفين فى pi  (النسبة التقريبية)

pi r² = pi(s-a)(s-b)(s-c)/s

مثال : اذا كانت أضلاع المثلث هى : 9 , 7 , 5

s = (5+7+9)/2 = 10.5   وبالتالى فإن :

Area of circle = pi (10.5 - 5)(10.5 - 7)(10.5 - 9)/10.5 = 11pi/4 ≈ 8.64‏