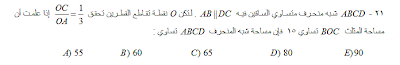1 اوجد اصغر عدد صحيح يحقق الشروط الآتية

اوجد اصغر عدد صحيح موجب الذى اذا قسم على 2
كان الباقى 3 واذا قسم على 5 كان الباقى 2 واذا قسم
على 3 كان الباقى 5 واذا قسم على 7 كان الباقى 11


ربما فهمت انك تقصد مبرهنة الباقى الصينية
نفرض ان العدد المراد هو x فيكون بذلك ..

  (1) ... x ≡ 3 (mod2)
x ≡ 2 (mod5) ... (2)
x ≡ 5 (mod3) ... (3)
x ≡ 11 (mod7) ... (4)

ll

لاحظ انه لا توجد عوامل مشتركة بين :
(2 ، 3) ، (5 ، 2) ، (3 ، 5) ، (7 ، 11)
، (3 ، 7)

 from (1) we find that x = 3+2r ... (5)
by substitution in (2)

3+2r ≡ 2 (mod5) ... (2)

2r ≡ -1 (mod5)
2r ≡ 4 (mod5)
r ≡ 2 (mod5)
r = 2 + 5s
by substitution in (5)
x = 3+2r ... (5)
x = 3+2(2+5s)
x = 3+4+10s
x=7+10s ... (6)
by substitution in (3)
x ≡ 5 (mod3) ... (3)

7+10s ≡ 5 (mod3) ... (3)
10s ≡ -2 (mod3)
10s ≡ 10 (mod3)
s ≡ 1 (mod3)
s = 1+3t
x=7+10s ... (6)
x = 7+10(1+3t)
x = 7+10+30t
x = 17+30t  ... (7)
by substitution in (4)
x ≡ 11 (mod7) ... (4)

17+30t ≡ 11 (mod7)
30t ≡ -6 (mod7)
30t ≡ 1 (mod7)
2t ≡ 1 (mod7)
2t ≡ 8 (mod7)
t ≡ 4 (mod7)
t = 4+7u
by substitution in (7)
x = 17+30t  ... (7)
x = 17+30(4+7u)
x = 17+120+210u
x = 137+210
x ≡ 137 (mod210)
ll

وهذا معناه ان اصغر عدد صحيح موجب
يحقق المطلوب هو  137

تابع القراءة

0 اوجد int (sin(x)+1)/cos(x)+1) dx

int (sin(x)+1)/cos(x)+1) dx
= - int  -sin(x)/(sox(x)+1) dx + int 1/(cos(x)+1) dx

= -ln|cos(x)+1| + int 1/(cos(x)+1) dx

but 1/(cos(x)+1) = 1/(2cos²(x/2)+1-1)

= 1/(2cos(x/2)) = ½sec²(x/2)

let  x/2 = u    then   dx = 2 du   by substitution ..

= -ln|cos(x)+1| + int sec²(u) du

= -ln|cos(x)+1| + tan(u) + c

but  u = x/2    by substitution to figure out ..

int (sin(x)+1)/cos(x)+1) dx = tan(x/2) - ln|cos(x)+1| + c‏

▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓

.
       جاس + 1
∫ ــــــــــــــــــــــــــ دس
      جتاس + 1


          - جاس                          1
= -∫ ـــــــــــــــــــــ دس + ∫ ــــــــــــــــــــــــــ دس
       جتاس + 1                   جتاس + 1

التكامل الأول = - لط ( مقياس المقام )
والتكامل الثانى ،نقوم بفك جتاس

           1                          
ــــــــــــــــــــــــــــــــــــــ = ½ جتا²(س/2)
2جتا²(س/2) - 1 + 1

= ½ قا²(س/2)   ثم نكامل بالتعويض ، وبفرض ان

         س                 دص          1
ص = ـــــــــــ   ، ومنها  ــــــــــ = ــــــــــ
         2                   دس         2

اى ان : دس = 2 دص ، بالتعويض ..

½∫ قا²(س/2) دس = ∫قا²(ص) دص

= ظاص    ولكن ص = س/2

اذاً قيمة التكامل الثانى = ظا(س/2)

بالعدوة الى التكامل الاصلى ....

       جاس + 1
∫ ــــــــــــــــــــــــــ دس
      جتاس + 1

= ظا(س/2) - لط(جتاس + 1) + ث

تابع القراءة

0 اوجد تكامل 2س * [جاس]^4 دس

∫2س جا^4(س) دس

اولاً نفك المقدار جا^4(س)

جا^4(س) = [جا²س]²

= [½(1-جتا2س)]²

= [¼(1 - 2جتا2س + جتا²(2س)]

= [¼(1 - 2جتا2س + ½(1+جتا(4س)]

= ¼ - ½جتا2س + ⅛(1+جتا(4س)

= ¼ - ½جتا2س + ⅛ + ⅛جتا(4س)

= ⅜ - ½جتا2س + ⅛جتا(4س)

نقوم بضرب ذلك المقدار فى س ، فيصبح

= ⅜س - ½س جتا2س + ⅛س جتا(4س)

ويتضح من خلاله ان التكامل اعلاه ..
∫2س جا^4(س) دس =

2[⅜∫س دس - ½∫س جتا2س دس + ⅛∫س جتا(4س) دس ]

نأخذ كل تكامل على حدى .. اولاً
⅜∫س دس = 3\16 س²

التكامل الثانى :

- ½∫س جتا2س دس

نفرض ان : ف = س
اذاً : دف = دس
، وان : دق = جتا2س دس
بمكاملة الطرفين ..

ق = ½ جا2س ،، بالتعويض ..

- ½∫س جتا2س دس

= -½[½س جا2س - ½∫جا2س دس ]

=  -½[½س جا2س + ¼ جتا2س]

= -¼ س جتا2س - ⅛جتا2س

وأخيراً نوجد التكامل الأخير ..
⅛∫س جتا(4س) دس

نضع : ف = س ، ومنها دف = دس
دق = جتا(4س)دس ومنها ق =¼ جا(4س)

⅛∫س جتا(4س) دس

= ⅛[¼س جا(4س) - ¼ ∫جا(4س) دس]

= ⅛[¼س جا(4س) + (1\16)جتا(4س) ]

= (1\32) س جا(4س) + (1\128) جتا(4س)

اذاً التكاملا اعلاه .. ∫2س جا^4(س) دس

= 2[ 3\16 س² -¼ س جتا2س - ⅛جتا2س
+(1\32) س جا(4س) + (1\128) جتا(4س)] + ث

تابع القراءة

1 ما هو تكامل قا^ن (س) ؟

 التكامل يتم بالتجزىء اذاً كانت درجة الأس فردية
اما اذا كانت زوجية كما فى مثالك هذا ..

∫ قا^8(س) دس

= ∫ قا²س . (قا²س)³ دس

= ∫ قا²س . (1 + ظا²س)³ دس

استعمل نظرية ذات الحدين ..

= = ∫ قا²س . (1+3ظا²س+3ظا^4س+ظا^6(س) ) دس

نفرض ان ظاس = ص  نفاضل الطرفين بالنسبة  لـ س

دص                             دص
ــــــ = قا²س   اذاً دس = ـــــــــــ
دس                           قا²س

بالتعويض ...

∫ (1+3ص²+3ص^4+ص^6 ) دص

والتكامل عادى جداً ..

= ص + ص³ + 3\5 ص^5 + 1\7 ص^7  + ث

ولكن ص = ظاس  بالتعويض

= ظاس + ظا³س + 3\5 ظا^5س + 1\7 ظا^7س + ث

حيث ث ثابت التكامل .. اى ان الصيغة العامة اذا كانت
درجة الأس ( ن مثلاً زوجية )

∫ قا^ن(س) دس

= ∫قا²س . (1 + ظا²س)^(ن/2 - 1)

وبعذ ذلك تستعمل نظرية ذات الحدين، ثم
تكامل بالتعويض .... وهكذا
ويمكن اثبات ذلك بالإستقراء على ن  ..

 

مثال اذا كانت درجة ن فردية :

∫قا^5(س) دس

= ∫قا²س قا³س دس

نفرض ان : ف = قا³س  بمفاضلة الطرفين
بالنسبة لـ س

دف
ــــــ = 3قا³س ظاس
دس

اذاً : دف = 3قا²س ظاس دس

ونفرض ان : دق = قا²س دس بمكاملة الطرفين
بالنسبة لـ س

ق = ظاس

اذاً:

∫قا^5(س) دس

= قا³س ظاس - 3∫ظا²س قا³س دس


= قا³س ظاس - 3∫ قا³س ( قا²س - 1 )  دس

= قا³س ظاس - 3∫ (قا^5(س) - قا³س )  دس

= قا³س ظاس - 3∫ قا^5(س) دس + 3 ∫ قا³س  دس

ولكن ∫ قا^5(س) دس = التكامل الأصلى ..
نفرض انها = م

4م =  قا³س ظاس + 3 ∫ قا³س  دس

اذاً :

∫قا^5(س) دس

= ¼ (قا³س ظاس + 3 ∫ قا³س  دس )

كامل مرة أخرى قا³س

▓ ولتعميم تلك القاعدة على التكامل بالتجزىء فقط نفعل ما يلى ▓


∫قا^ن (س) دس

= ∫ قا²س . قا^(ن-2) (س) دس

نفذ نفس الخطوات السابقة ..
نفرض ان : ف = قا^(ن-2) (س)

 
اذاً : دف = (ن-2) قا^(ن-2) (س) ظا(س) دص

دق = قا²س دس  ومنها ق = ظاس

بالتعويض .. التكامل اصبح ...

قا^(ن-2) (س) ظاس - ∫ (ن-2) قا^(ن-2) (س) ظا²س دس

= قا^(ن-2) (س) ظاس -
(ن-2)∫ قا^(ن-2) (س) (قا²س - 1 ) دس

= قا^(ن-2) (س) ظاس -
(ن-2)∫ قا^ن (س) + (ن-2) ∫ قا^(ن-2) (س)  دس

= قا^(ن-2) (س) ظاس -
(ن-2)∫ قا^ن (س) دس
+ (ن-2)∫ قا^(ن-2) (س)  دس

نفرض ان التكامل الأصلى = م

م = قا^(ن-2) (س) ظاس
- (ن-2)∫ قا^(ن-2) (س)  دس

(ن-1) م = قا^(ن-2) (س) ظاس
+ (ن-2)∫ قا^(ن-2) (س)  دس

م = 1/(ن-1) قا^(ن-2) (س) . ظا(س)
+ (ن-2)/(ن-1)∫ قا^(ن-2) (س)  دس

 int sec^n(x)dx=1/(n-1) sec^(n-2)(x) tan(x) + (n-2)/(n-1)
∫ sec^(n-2) dx


ثم كرر نفس الخطوات السابقة اذا
تطلب الأمر تجزىء اكثر من مرة ..
وهذه هى الصيغة العامة لإجراء
اى تكامل على هذه الشاكلة

∫قا^ن (س) دس

تابع القراءة

0 ما هو تكامل 3س/(س² -2س + 5) دس ؟

.                3س
∫ ـــــــــــــــــــــــــــــــــــــــــ دس
         س² - 2س + 5

بأخذ 3 خارج التكامل، فيصبح :-

                س
3 ∫ ـــــــــــــــــــــــــــــــــــــــــ دس
         س² - 2س + 5


بالضرب فى 2 ثم القسمة عليها مرة أخرى ..

  3                2س
ـــــــ  ∫ ــــــــــــــــــــــــــــــــ دس
  2         س² - 2س + 5

بضرح 2 من البسط ثم جمعها مرة أخرى ..

  3              2س - 2 + 2
ـــــــ  ∫ ــــــــــــــــــــــــــــــــ دس
  2         س² - 2س + 5

بتوزيع البسط على المقام ..

      3        2س - 2                            2
= ـــــــ [∫ـــــــــــــــــــــــــ دس +∫ـــــــــــــــــــــــــــــ دس ]
     2      س² - 2س + 5             س² - 2س + 5

لاحظ ان التكامل الأول يعتبر البسط مشتقة المقام
وقيمته = لط (س² - 2س + 5 )

                                       3
لاحظ معى : سأهمل مؤقتاً الـ ـــــــ المضروبة
                                       2
فى التكامل . وسأهمل ايضاً قيمة التكامل الأول
والذى = لط (س² - 2س + 5 )
فلا اريد تكرارهم فى الخطوات التالية، وسنركز فقط
على :
           2
∫ـــــــــــــــــــــــــــــ دس
  س² - 2س + 5


بالقسمة بسطاً ومقاماً على 4 ( لماذا ؟؟ حاول ان تبحث
عنها بنفسك حيث اننا نهدف الى صيغة بعينها )

                 ½
∫ــــــــــــــــــــــــــــــــــــــــــــــــ دس
  1\4 س² - ½ س + 1\4  +  1

لاحظ ان المقدار :  1\4 س² - ½ س + 1\4
عبارة عن مربع كامل = (½س - ½)²

اذاً التكامل اعلاه اصبح : -

                 ½
∫ــــــــــــــــــــــــــــــــــــــــــــــــ دس
        (½س - ½)²  +  1

تماماً هى الصيغة التى نريدها وقيمة هذا التكامل
= الظل العكسى لـ للزاوية (½س - ½ )

نأتى الى التكامل من اوله.. اذاً

                 3س
∫ ـــــــــــــــــــــــــــــــــــــــــ دس
         س² - 2س + 5

     3                                   -1
= ـــــــ [لط|س² - 2س + 5| + ظا (½س - ½ )] + ث
     2

حيث لط هو ln بالإنجليزى ، او اللوغاريتم الطبيعى
وظا^-1  هو الظل العكسى ، ث هو ثابت التكامل

تابع القراءة

0 اوجد النهاية الآتية بدون استعمال قاعدة لوبيتال، او حتى منشور ماكلورين

                        جاس  -  س
      نهـــــــــا ــــــــــــــــــــــــــــــــــــــ
     س ← 0            س^5

الحل : نفرض ان : س = 5ص  فعندما تؤول س الى الصفر فإن 5ص تؤول ايضاً الى اصلفر
ومنها نستنتج ان  ص تؤول الى الصفر ..

                    جا5ص   -  5ص
نهـــــــــــــا ــــــــــــــــــــــــــــــــــــــــــــــــــ
ص← 0         3125 ص^5

وبتطبيق المتطابقة  جا5ص = 16جا^5(ص) - 20جا³(ص) + 5جا(ص)
والإثبات على هذا الرابط

                     16جا^5(ص) - 20جا³(س) + 5جا(س) - 5ص    
= نهــــــــــــــا ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
   ص← 0                     3125 ص^5

وبتوزيع البسط على المقام ( لكن بترتيب وهدف معين وضعناه فى الحسبان )
         

        16                       جاص                  4                      جاص            1                      جاص  - ص
= ـــــــــــــــــ  نهـــــــــــا (ـــــــــــــــــ )^5  - ــــــــــــــــــ نهـــــــــــا (ــــــــــــــ)³ + ـــــــــــ نهــــــــــا ـــــــــــــــــــــــــــــــــــ
      3125    ص←0      ص                 625 ص²  ص←0       ص          625   ص←0           ص


نلاحظ ان : جاص/ص = 1  عندما ص تؤول الى الصفر ، وايضاً نلاحظ الآتى:

                                     جاص  -  ص
المقدار :  نهــــــــــــــــا  ـــــــــــــــــــــــــــــــــــــــــــــــ يعكس تماما ً نفهوم النهاية الأصلية، لكن مع تغيير س الى ص فقط
             ص←0                  ص ^5               وبفرض ان النهاية الاصيلة = ن ، فإن هذا المقدار ايضاً  = ن

                            -4
وايضاً  نهـــــــــــا  ــــــــــــــــــــ = - ∞
         ص←0      625 ص²

من خلا ما سبق نستنتج ان :

             16                              1
ن =  ـــــــــــــــــــــ  = - ∞ + ـــــــــــــــــــــ  ن
           3125                          625

              1
ن ( 1 - ــــــــــــ ) = - ∞
            625

وهذا معناه ان  ن  ايضاً  = - ∞


اذاً :                  جاس  -  س
      نهـــــــــا ــــــــــــــــــــــــــــــــــــــ = - ∞
      س ← 0          س^5

تابع القراءة

0 اثبت ان جا(5س) = 16جا^5(س) - 20جا³(س) + 5جا(س)

يعتمد الإثبات فى الأساس على قانون مجموع زاويتين لدالة الجيب، وايضاً قانون ضعف الزاوية
والقانون :  جتا²س = 1 - جا²س ،  ... الخ

جا(5س) = جا(4س+س) = جا4س جتاس + جتا4س جاس

= 2جا2س جتا2س جتاس + جتا4س جاس

 = 2جاس جتا²س جتا2س + جاس (جتا²(2س) - جا²(2س) )

= 4جاس جتا²س [1 - 2جا²س] + جاس [(1 - 2جا²س )² - 4جا²س جتا²س]

= 4 جاس ( 1 - جا²س) (1 - 2جا²س) + جاس [ 1 - 4جا²س  + 4جا^4(س) - 4جا²س (1 - جا²س) ]

= 4 جاس [2جا^4(س) - 3جا²س + 1 ]  + جاس [ 1 - 4جا²س + 4جا^4(س) - 4جا²س + 4جا^4(س) ]

= 8جا^5(س) - 12جا³س + 4جاس + جاس ( 8جا^4(س) - 8جا²س + 1)

= 8جا^5(س) - 12جا³س + 4جاس +  8جا^5(س) - 8جا³س + جاس

= 16جا^5(س) - 20جا³(س) + 5جا(س)

تابع القراءة

0 اوجد العدد جـ²(أ+ب) اذا علمت ان ....

بفرض ان أ ، ب ، جـ ثلاثة اعداد حقيقية مثنى تحقق أ² (ب+جـ) = ب² (أ+جـ) = 2009
فإن العدد جـ² (أ+ب) = ؟؟

الحل :
أ² (ب+جـ) = 2009   اذاً   أ² ب + أ² جـ = 2009                     (1)
ب² (أ+جـ) = 2009   اذاً   أ ب² + ب² جـ = 2009                    (2)

بضرب (1) فى ب  ،  وضرب (2) فى أ  فينتج لدينا نظامين، وهما

أ² ب² + أ² ب جـ = 2009 ب                  (3)
أ² ب² + أ ب² جـ = 2009 أ                    (4)

ـــــــــــــــــ بطرح (3) ، (4) ـــــــــــــــــــــــــ

أ² ب جـ - أ ب² جـ = 2009ب - 2009 أ      ومنها نحصل على

أ ب جـ ( أ - ب ) = 2009 ( ب - أ )         اى ان :

أ ب جـ ( أ - ب ) = - 2009 ( أ - ب )      بقسمة الطرفين على ( أ - ب ) فنحصل على

أ ب جـ = - 2009                                (5)

بعد ان حصلنا على معادلة (5) نقوم بجمعها مع معادلة (1)

أ² ب + أ² جـ = 2009                     (1)
أ ب جـ = - 2009                           (5)

ــــــــــــــــــ بالجمع ــــــــــــــــــــــــــــــــ

أ² ب + أ² جـ + أ ب جـ = 0      بقسمة الطرفين على أ

أب + أجـ + ب جـ = 0      اذاً  جـ (أ+ب) + أ ب = 0

ثم :    جـ (أ+ب) = - أ ب          بضرب الطرفين فى  جـ

جـ² (أ+ب) = - أ ب جـ      ولكن : أ ب جـ = - 2009         (5)

اى ان : - أ ب جـ = 2009

اذاً  :  جـ² (أ+ب) = 2009

تابع القراءة

7 ايجاد مساحة اى شكل منتظم عدد اضلاعه ن

ولنثبت صحة القانون
حيث اننا نأتى من مركز الشكل المنتظم، وكل ضلع
من اضلاعه يحمل مثلث متساوى الساقين، ونريد ان نوجد
مساحة هذا الشكل المنتظم بدلالة طول القاعدة، والإرتفاع
ولكن الأإرتفاع مجهول، لذلك وجب علينا ان نوجد الإرتفاع
بدلالة الزاوية ( هـ )  ، فنفرض ان طول حرفه س

مساحة المثلث = ½ طول القاعدة فى الإرتفاع

                   = ½ س × ع
                                                          ½ س
حيث ع اقصد به الإرتفاع ، ولكن  ظا(هـ/2) = ــــــــــــــــــ
                                                           ع

                   ½س
ومنها  ع = ـــــــــــــــــــــــ      بالتعويض
                ظا(هـ/2)

                                      ½س
مساحة المثلث = ½ س × ـــــــــــــــــــ
                                    ظا(هـ/2)
          س²
= ــــــــــــــــــــــــ
     4 ظا(هـ/2)

ولكن هذه مساحة مثلث واحد فقط ، اذاً مساحة اى شكل منتظم
عدد اضلاعه  ن ضلعاً

        ن س²
= ــــــــــــــــــــــــ
     4 ظا(هـ/2)

حيث هـ هى الزاوية بين اى ساقين، ويمكن ايجادها من خلال هذا القانون

                 180 (ن-2)

هـ = ـــــــــــــــــــــــــــــــــــــــــــــــــــــ

                       ن

تابع القراءة

1 اثبت ان نها(س←0 ) جاس/س = 1

بالنظر الى الرسم نجد ان فى دائرة الوحدة طول الضلع
المقابل للزاوية س هو جاس، حيث س قياس الزاوية
بالتقدير الدائرى، وهذا معناها ان القوس الذى يحمل
الزاوية = س ( بالتقدير الدائرى )

سنركز على ثلاث علاقات وهما مساحة المثلث
المتساوى الساقين، ومساحة القطع الدائرى
ومساحة المثلث القائم الكبير ..

حيث ان مساحة المثلث المتساوى الساقين اقل من مساحة القطع الدائرى
اقل من مساحة المثلث القائم ..

اولاً : مساحة المثلث المتساوى الساقين = ½ جاس
ثانياً : مساحة القطع الدائرى = ½س
ثالثاً : مساحة المثلث القائم = ½ ظاس

اذاً :  ½جاس < ½س < ½ظاس بقسمة جميع الاطراف على ½

جاس < س < ظاس     بقسمة جميع الاطراف على جاس

         س        ظاس
1 < ــــــــــــ < ــــــــــــ
       جاس       جاس

لاحظ ان ظاس / جاس = 1/جتاس



         س           1
1 < ــــــــــــ < ــــــــــــ       عندما نقلب جميع الاطراف نغير علامات التباين
       جاس       جتاس

         جاس
1 > ـــــــــــــــــ > جتاس
          س

ثم لاحظ ان جتاس  تقترب من الواحد الصحيح كلما اقتربت س من الصفر
اذاً :

         جاس
1 > ـــــــــــــــــ > مقدار يتقرب جداً من الواحد الصحيح
          س

                       جاس
اذاً : نهــــــــــا ــــــــــــــــــــ = 1
     س←0           س

تابع القراءة

0 اثبت ان مشتقة جاس = جتاس

د(س) = جاس        ، دَ(س) = ؟؟


               جا(س+هـ) - جاس
نهــــــــــا ــــــــــــــــــــــــــــــــــــــــــ
هـ←0                 هـ


                  جاس جتاهـ + جتاس جاهـ - جاس
= نهــــــــــا ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
     هـ←0                       هـ


                  جاس(جتاهـ - 1) + جتاس جاهـ
= نهــــــــــا ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
     هـ←0                       هـ

                         (جتاهـ - 1)                               جاهـ
= جاس نهــــــــا ــــــــــــــــــــــــــــــــــ +جتاس نهــــــا ــــــــــــــــ
           هـ←0           هـ                        هـ ←0       هـ


ولكن هناك نهاية شهيرة جداً ( فى درس نهاية الدوال المثلثية عند الصفر )
تقتضى ان نهـــــــا لما (هـ تؤوول الى 0 ) (جتاهـ - 1 ) هـ = 0
وايضاً نهــــا   لما (هـ تؤوول الى 0 ) جاهـ /هـ = 1

وبناء عليه تكون النهاية السابقة = جتاس  ( وهو المطلوب )

تابع القراءة

0 اوجد مساحة شبه المنحرف المبين بالرسم

أ ب جـ د شبه منحرف متساوى
الساقين، أ ب يوازى دجـ ، لتكن و نقطة تقاطع قطريه بحيث
تحقق العلاقة  وأ / وجـ = 1\3   (( هذه الخطوة للتصحيح ))
فإذا علمت ان مساحة المثلث ب و جـ = 15 فإن مساحة
شبه المنحرف أ ب جـ د = ؟؟

الحل : تعريفات لن اذكرها .. جاو = جا الزاوية المكملة لها
مساحة المثلث = ½ حاصل ضرب طول اى ضلعين فى جيب
الزاوية المحصورة بينهم .. ، نظرية هامة فى الهندسة المستوية
اذا رسما مثلثان على قاعدة وفى جهة واحدة منها ، ينحصران
بين مستقيمين متوازيين، كانا متساويان فى المساحة ( على ما اذكر )

اذاً : مساحة المثلث أ د جـ = مساحة المثلث ب د جـ
ولكن المثلث و د جـ ( مشترك بينهم ) اذاً مساحة المثلث
أ و د = مساحة المثلث ب و جـ = 15

وايضاً هناك تشابه بين المثلثين و أ ب ، و د جـ  حيث يحقق
ان ( خطوة لن اذكرها وهى عبارة نسب بين اطوال اضلاع )
نستنتج منها ما هو موضح بالرسم ..

نأتى الى المثلث الذى مساحته 15 وحدة مربعة
حيث نستنتج منه الآتى : ½ 3 م² جاو = 15
اذاً : م² جاو = 10  ومنها  :

             10
جاو = ــــــــــــــ
             م²


الآن وبكل بساطة نستطيع ايجاد مساحة كلاً من المثلثين و د جـ ، و أ ب
اولاً مساحة المثلث و أ ب = ½ م² جاو  بالتعويض عن جاو

                                      10
مساحة المثلث = ½ م² × ـــــــــــــ = 5 وحدات مربعة
                                     م²

                                                 10
مساحة المثلث و د جـ = ½ 9 م² × ــــــــــــــ = 45 وحدة مربعة
                                                 م²


اذاً مساحة شبه المنحرف أ ب جـ د = (2×15) + 45 + 5 = 80 وحدة مربعة

تابع القراءة

0 ادرس اشتقاق الدالة الآتية د(س) = أس³ + ب س² + جـ س + د من حيث ...

برهن اذا امتلكت الدالة : د(س) = أس³ + ب س² + جـ س + د
نقطتين حرجتين فان نقطة الانقلاب تقع في منتصف المسافة بينهما واذا امتلكت نقطة حرجة واحدة فقط فهي نقطة انقلاب .
الحل : -



د(س) = أس³ + ب س² + جـ س + د
دَ(س) = 3أس² + 2ب س + جـ
دً(س) = 6أس + 2ب
ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
الإحتمال الأول انها دالة تمتلك نقطتين حرجتين، نساوى المشتقة
الأولى بـ صفر .

3أس² + 2ب س + جـ = 0

الحل بالقانون العام : المميز = جذر(4ب² - 12أجـ) = 2جذر(ب² - 3أجـ)

            -2ب ± 2جذر(ب² - 3أجـ)             -ب ± جذر(ب² - 3أجـ)
س = ـــــــــــــــــــــــــــــــــــــــــــــــــ = ــــــــــــــــــــــــــــــــــــــــــــ
                      6أ                                        3أ

ولكن متصف الإحداثى السينى لهما

     -ب + جذر(ب² - 3أجـ)     -ب - جذر(ب² - 3أجـ)
= ـــــــــــــــــــــــــــــــــــ + ـــــــــــــــــــــــــــــــــــــ
           6أ                               6أ

     -2ب         -ب
= ـــــــــــ = ـــــــــــــــــ
     6أ           3أ

من أخرى نقطة الإنقلاب نستنتجها من خلال تصفير المشتقة الثانية ..
6أس + 2ب = 0  ومنها 6أس = -2ب  ، ومنها  3أس = -ب

                    -ب
ومنها  س = ـــــــــــــــ = نقطة المنتصف للنقطتين الحرجتين ( المطلوب الأول )
                     3أ


المطلوب الثانى اذا تحقق يتحقق معه الآتى :-
يجب ان تكون المشتقة الأولى عبارة عن مربع كامل ( لماذا ؟ )
ولما كانت المشتقة الأولى عبارة عن مربع كامل فإن ما تحت الجذر = 0
او بمعنى ادق المميز = 0

          -ب
س = ـــــــــــ = نقطة المنتصف ( فى المطلوب الأول )
          3أ

وهى بمثابة نقطة انقلاب فى حالة مساواه المشتقة الثانية بـ صفر .

تابع القراءة

1 اوجد النهاية الآتية بدون قاعدة لوبيتال نها(س←2) (3^س - 9)/(2^س - 4)

نفرض ان : 3^س = ص  بأخذ لو الطرفين  لو3^س = لوص ، ومنها س لو3 = لوص
، ومنها  س = لوص/لو3 =  لوص     (( متطابقة (1) فى اللوغاريتمات ))
                                     3

اذاً : 2^س = 2^لوص    =  ص^لو2    (( متطابقة (2) فى اللوغاريتمات ))
                      3                   3

وعندما س = لوص  ، فإن  لوص ← 2   ومنها  ص ← 9
                  3                3

بالتعويض فى النهاية الأصلية وهى : -

                      3^س - 9                                              ص - 9
نهـــــــــــا ـــــــــــــــــــــــــــــــــــــــــــــــ = نهــــــــــــــــــا ـــــــــــــــــــــــــــــــــــــــــ
س←2            2^س - 4                    ص←9         ص^لو2   - 4
                                                                                 3


لاحظ عندما ص ← 9   فإن  جذر(ص) ← 3

                               جذر(ص)  - 3                             جذر(ص) + 3
= نهـــــــــــــــــــــــا ــــــــــــــــــــــــــــــــــــــــــــــــــ × ـــــــــــــــــــــــــــــــــــــــ
   جذر(ص)←3      جذر(ص)^لو2  - 2                  جذر(ص)^لو2  + 2
                                          3                                         3


تعتبر نهايتين مضروبين فى بعض، وعند التعويض فى النهاية الثانية  نجدها = 3\2

                                               جذر(ص)  - 3
= 3\2 × نهـــــــــــــــــا ــــــــــــــــــــــــــــــــــــــــــــ
           جذر(ص)←3       جذر(ص)^لو2   -  2
                                                      3

لاحظ انه يمكن وضع  2 = 3^لو2         (( متطابقة  (3) فى اللوغاريتمات ))   ، وبالتعويض
                                      3

                                              جذر(ص)  - 3              
= 3\2 × نهـــــــــــــــــا ــــــــــــــــــــــــــــــــــــــــــــ
           جذر(ص)←3      جذر(ص)^لو2   -  3^لو2
                                                     3             3

المسألة اصبحت جاهزة تمامً لتطبيق نظرية " 4 "  فى التفاضل ( الإثبات من هنا )

                     1
= 3\2 × ــــــــــــــــــ × 3^(1 - لو2 )
               لو2                    3
                3


        3                    3
= ــــــــــــــــ  × ــــــــــــــــــــــــــ
     2لو2                3^لو2
       3                      3


لاحظ ان :  3^لو2 = 2      بالتعويض
                  3

          9                9
= ــــــــــــــــــــ = ـــــــــــ  لو3
      4 لو2              4     2
          3


وهى نفس النهاية التى ستحصل عليها اذا حليت المسألة 
بقاعدة لوبيتال .. المصدر مأخوذ من حل الأخ Khaled Einstein
على شبكة التواصل الإجتماعى فيسبوك .

تابع القراءة

0 اثبت ان جا(3س) = 3جاس - 4جا³س

يعتمد الإثبات على عدة اساسيات منها جا ضعف الزاوية

حيث ان جا2س = 2جاس جتاس ، وان جتا2س = جتا²س - جا²س

= 1 - 2جا²س  ، ومتطابقات أخرى معروفة ..

جا3س = جا(2س + س)  = جا2س جتاس + جتا2س جاس

= 2جاس جتا²س + (1-2جا²س ) جاس

= جاس [2جتا²س + 1 - 2جا²س]

ولكن : جتا²س = 1 - جا²س  ( حسب دائرة الوحدة )

= جاس [ 2 - 2جا²س + 1 - 2جا²س]

= جاس [ 3 - 4جا²س]  = 3جاس - 4جا³س       (( وهو المطلوب ))

تابع القراءة

9 اوجد النهاية الآتية نها(س←0) (س - جاس)/س³

اوجد :                       س - جاس
         نهـــــــــــا ــــــــــــــــــــــــــــــــــــــ
         س←0           س³
الحل الأول عن بإستعمال قاعدة لوبيتال
وبعد مرحلة الإشتقاق اصبحت المسألة
على هذا الشكل .


نهـــــــــا ( 1 - جتاس )/3س² = 0/0 عدم تعيين
س←0


نشتق مرة أخرى كلاً من البسط والمقام..


= نهـــــــــا جاس/6س = 0/0  نشتق مرة أخرى ..
   س←0


= نهــــــــــا جتاس/6  وبوضع س = 0  نجد النهاية = 1\6
    س←0




الطريقة الثانية بإستعمال متسلسلة ماكلورين :-




جاس = س - س³/3! + س^5/5! - س^7/7! + ....

بضرب الطرفين فى -1

-جاس = -س + س³/3! - س^5/5! + س^7/7! - .....

بإضافة س للطرفين

س - جاس = س³/3! - س^5/5! + س^7/7! - .....

وبقسمة الطرفين على س³

(س - جاس)/س³ = 1\3! - س²\5! + س^4\7! - ......

وبوضع س = 0

(س - جاس)/س³ = 1\3! + ( مجموعة اعداد تؤول الى الصفر )

=1\3! = 1\6

حل آخر بدون استعمال قاعدة لوبيتال، او منشور ماكلورين




نفرض ان  س = 3ص وعندما 3ص ←0 فإن ص ←0
، وبفرض ان النهاية = ن




                   3ص - جا3ص                             3ص - جا3ص
نهــــــــــا ــــــــــــــــــــــــــــــــــــــــ = 1\27  ـــــــــــــــــــــــــــــــــــــــــــــ
ص←0             27ص³                                       ص³


ولكن جا3س = 3جاس - 4جا³س  ( متطابقة اثباتها فى تصنيف حساب مثلثات )


                       3ص - [3جاص - 4جا³ص]
1\27نهــــــــــــــا ـــــــــــــــــــــــــــــــــــــــــــــــــ
      ص←0                     ص³




                                    3ص - 3جاص + 4جا³ص
=1\27 نهــــــــــــــــــا ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
         ص←0                           ص³




بتوزيع البسط على المقام ينتج :


                       3 (ص - جاص )               4جا³ص      
1\27نهـــــــــــــا ـــــــــــــــــــــــــــــــــــــ + ـــــــــــــــــــــ
      ص←0              ص³                         ص³


                              ص - جاص                                   جاص
= 1\27(3 نهــــــــــــا ـــــــــــــــــــــــــــ + 4 نهـــــــــــــا[ ــــــــــــــــــــــ ]³       )
             ص←0          ص³                   ص←0              ص      




ولكن النهاية الأولى = ن   


 ن = 1\27 ( 3ن + 4 )


           ن               4 
ن = ـــــــــــــ  + ــــــــــــــــــ     
          9              27




27ن = 3ن + 4   ، ومنها  24ن = 4   اذاً : ن = 1\6

تابع القراءة

0 اوجد النهاية الآتية نهـا(س←2) (2^س -4)/(س-2)

اوجد :                       2^س - 4
           نهــــــــــا ــــــــــــــــــــــــــــــــــ
            س ←2          س -2

الحل الأول :( بإستعمال قاعدة لوبيتال )

=  نهـــــــــا 2^س × لط 2 = 4 لط2
     س←2

( حيث لط اللوغاريتم الطبيعى )

الحل الآخر بمنشور تايلور :-

نهـا(س←2) (2^س - 4) / (س-2)

نفرض ان : د(س) = 2^س ، ومنها
دَ(س) = 2^س لط2
دً(س) = 2^س (لط2)²
دً َ (س) = 2^س (لط2)³ .... so on

وبنشر 2^س عندما تقترب س من 2

2^س = 4 + 4(لط2)(س-2)+2(لط2)²(س-2)²+4\3!(لط2)³(س-2)³+.....

بطرح -4 من الطرفين يتبقى لدينا

2^س - 4 = 4(لط2)(س-2)+2(لط2)²(س-2)²+4\3!(لط2)³(س-2)³+.....

بقسمة الطرفين على (س-2)

(2^س - 4 )/(س-2) = 4لط2 + 2(لط2)²(س-2) + 4\3!(لط2)³(س-2)²+...

وبوضع س = 2 نجد ان النهاية تقترب من 4 لط(2)
≈ 2.772588722

        

تابع القراءة

0 اوجد س توافيق ص

المسألة الأولى : [(س+ص) ل 2 ] = 42 ، [(س-ص) ل 2 ] = 20
المطلوب ايجاد  : س ق ص

[(س+ص) ل 2 ] = 42        اذاً

      (س+ص)!
ــــــــــــــــــــــــــــــــ = 42
    (س+ص-2)!

(س+ص) (س+ص-1)(س+ص-2)!
ــــــــــــــــــــــــــــــــــــــــــــــــــــ = 42
          (س+ص-2)!


(س+ص) (س+ص-1) = 42               (1)

      (س-ص)!
ــــــــــــــــــــــــــــــــــــ = 20
     (س-ص-2)!

(س-ص) (س-ص-1) (س-ص-2)!
ــــــــــــــــــــــــــــــــــــــــــــــــــــ = 20
              (س-ص-2)!

(س-ص) (س-ص -1) = 20

(س-ص)² - (س-ص) = 20        (2)

بترتيب (1) ، (2)

(س+ص) (س+ص-1) = 42               (1)

(س+ص)² - (س+ص) = 42

س² + 2س ص + ص² - س - ص = 42

س² + ص² + 2س ص - س - ص = 42            (1)

(س-ص)² - (س-ص) = 20        (2)

س² - 2س ص + ص² - س + ص = 20         (2)
س² + ص² + 2س ص - س - ص = 42         (1)

ـــــــــــــــــــــــــ بجمع (1) ، (2) ـــــــــــــــــــــــــــــــــــ
2س² + 2ص² -2س = 62

س² + ص² - س = 31   بالتعويض فى (1)

س² + ص² + 2س ص - س - ص = 42         (1)

31 + 2س ص - ص = 42

2س ص - ص = 11
                                             11
ص (2س - 1 ) = 11   ،  ص = ـــــــــــــــــــــ            (3)
                                        (2س - 1)

بالتعويض فى س² + ص² - س = 31

                         11
س² - س + ــــــــــــــــــــــــــــ = 31
                    (2س - 1)


س²(2س-1) - س(2س-1) + 11 = 31(2س-1)

2س³ - س² - 2س² + س + 11 - 62س + 31 = 0

2س³ -3س² - 61س + 42 = 0

عوض بـ س=1 ، 2 ، 3 .... الى ان تصل الى س=6 فتجدها
تحقق المعادلة تماماً : فنقوم بقسمة المعادلة على (س-6)

2س² +9س -7
ـــــــــــــــــــــــــــــــــــــــــــــ
2س³ -3س² - 61س + 42   |  (س-6)
                                   ــــــــــــــــــــــــ
2س³ -12س²
ــــــــــــ بالطرح ــــــــــــــــــــــ
9س² -61س + 42
9س² - 54س
ــــــــ بالطرح ـــــــــــــــــ
-7س + 42
-7س + 42
ـــــــ بالطرح ــــــــــ
00            00

اذاً : احتمال : (2س² +9س -7) = 0
نحلها بالقانون العام
المميز = جذر(81 + 56) = جذر(137)

             -9 ± جذر(137)
س = ــــــــــــــــــــــــــــــــــــــ
                    4

اما س ≈ 1.4261749  ،  س ≈ -5.17617  ، واخيراً اما ، س = 6

نستثنى الأعداد النسبية، ونأخذ الحل س = 6  بالتعويض فى 3

                11                        11
ص = ــــــــــــــــــــــــــ  = ـــــــــــــــــــــــــــ = 1
            (2س - 1)               (12 - 1 )


اذاً :  س              6
           ق     =     ق  = 6
             ص           1

اعلم جيداً ان لها حل آخر، لكنه لا يحضرنى الآن ..

تابع القراءة

0 كيف نثبت ان جا2س = 2جاس جتاس ؟

نعلم من قانون مجموع زاويتين او الفرق بينهما ان : 


جا(س+ص) = جاس جتاص + جتاس جاص 
وبوضع  س = ص 


جا(س+س) = جاس جتاس + جتاس جاس


جا2س = 2 جاس جتاس      (( هـ . ط . ث ))


ملحوظة : نستطيع استنتاج اكثر من قانون للإثبات صحة 
هذه المتطابقة .


حتى لا يكون كلامنا عبارة عن هرطقان كلامية، اورد لك هذا
الإثبات ( الذى آراه من وجهة نظرى ) من اقوى، واروع وافضل
 الإثباتات لهذا القانون .. تابع


لنفرض وجود مثلث متساوى الساقين، طول ساقيه = الوحدة
والزاوية بين الساقين = 2س

نوجد مساحة المثلث بطريقتين، ثم نساويهم ببعض ..
مساحة المثلث = ½ 1 × 1 × جا2س = ½جا2س               (1)
ولكن مساحة المثلث ايضاً = ½ طول القاعدة × الإرتفاع


لاحظ لإيجاد نصف مساحة القاعدة والإرتفاع .. انظر الى صورة
المثلث المتساوى الساقين ستجد انه عبارة عن مثلثين قائمين، وبتطيق
جا2س = المقابل / الوتر ... الخ ( هذه القوانين جربها بنفسك )
المهم ستصل الى ان :  نصف القاعدة عبارة عن جاس، وان الإرتفاع
عبارة عن جتاس ..

مساحة المثلث  = ½ طول القاعدة فى الإرتفاع

=  جاس جتاس              (2)         اذاً علاقة (1) = علاقة (2)

½جا2س = جاس جتاس          وبضرب الطرفين فى 2 نحصل على المطلوب

جا2س = 2جاس جتاس

اذا كان عندك اثبات آخر لهذا القانون، فضعه حتى يستفيد منه الجميع .

تابع القراءة

0 ما الفرق بين المتطابقة - المعادلة - القانون ؟

المعادلة هى تساوى طرفين او اكثر،
(( فى مجموعة صغيرة من الأعداد ))
المتطابقة هى ايضاً تساوى طرفين او اكثر،
لكن فى مجموعة كبيرة من الأعداد تصل
فى اغلب الأحيان الى مجموعة الأعداد الحقيقية
والمركبة معاً ..!

القانون (( هو المفهوم للمتطابقة، وسؤالك رائع فى هذه النقطة ))

وحتى لا يكون مجرد كلام يكتب بدون تطبيق، فنقوم بتطبيق الآتى ..

س+ص = 1   هذه معادلة وليست متطابقة لماذا ؟؟ هل هى قانون ؟؟

لا يوجد اطلاقاً قانون مثل هذا ، انما هى معادلة او مجر ( فرضية )
ان هناك عددان س،ص ناتج جمعهما = 1  فتعطى عدد لا نهائى من الأعداد
((لكن هذه الأعداد ليست من اختيارنا )) بمعنى .. لا يجوز ان اقول وبوضع س = 3
، ص = 2  مثلاً ؟؟ لأنها لا تحقق شرط المعادلة ..


مثال2)  س² = -2س - 1   لا يجوز ان اقول وبوضع س =  5  مثلاً للطرفين

س² +2س + 1 = 0   ومنها  (س+1)² = 0   ومنها س = -1

اذاً  5 لا تحقق المعادلة ..


مثال3) جتا²س +جا²س = 1               (( هذا قانون او متطابقة ))

وبوضع س = ص² + 2ص + 1       للطرفين

(( طبعاً لاحظ ان الطرف الايسر لا يحتوى على س ))

جتا²(ص²+2ص+1) + جا²(ص²+2ص+1) = 1

وفى هذا المثال نستطيع ان نضع س تنتمى لأى مجموعة تختارها من الأعداد
حقيقية ، مركبة .. فعندما نكتب : جتا²س + جا²س = 0
فضع س كما تشار ، ولكن لاحظ ان هذا الكلام لا ينطبق على المعادلة
حيث ان المعادلة التى بها مجهول واحد اما ان يكون لها حل واحد، واما
ان تكون مستحيلة الحل ..

مثال4) جتاس - جتاص = -2جا½(س+ص) جا‎½(س-ص)

متطابقة مثلثية تحتوى على مجهولين س،ص

وبوضع س = ص    تحصل على المطلوب 0 = 0

وبوضع  س بـ س²+2س+1   ،  ص بـ س²-2س + 1

جتا(س²+2س+1 ) - جتا(س²-2س + 1)

= -2جا½(س²+2س+1 + س²-2س + 1) جا½((س²+2س+1 ) - (س²-2س + 1) )

= -2جا½(2س² + 2 ) جا½ (4س)

= -2جا(س²+1) جا(2س)

تابع القراءة

2 اوجد نهـا(ن←∞) م

م = 0.25ن × س² × ظا[( ن - 2 )( ط\2ن )]               (1)
نق = 0.5س × ظا[( ن - 2 )( ط \2ن )]                     (2)
اوجد نها م عند ن تؤول للمالانهايه

الحل : اولاً نوجد م بدلالة ن فقط، وهذا يتطلب منا ان نتخلص من س بدلالة ن كالـآتى : -

من العلاقة الثانية : نق = 0.5س × ظا( ( ن - 2 )( ط \2ن ))

                                      2نق
نجد ان س =  ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ  
                          ظا[( ن - 2 )( ط \2ن )]

 بالتعويض فى علاقة (1)
م = 0.25ن × س² × ظا[( ن - 2 )( ط\2ن )]               (1)

                               2نق
م = 0.25ن ×[ـــــــــــــــــــــــــــــــــــــــ  ]² × ظا[( ن - 2 )( ط\2ن )]
                   ظا[( ن - 2 )( ط \2ن )]


                   ن نق²
م = ـــــــــــــــــــــــــــــــــــــــ
        ظا[( ن - 2 )( ط \2ن )]
                                               ط          
سنعيد ترتيب زاوية الظل : ( ن - 2 )( ـــــــ )  = ط/2 - ط/ن
                                              2ن        


                 ن نق²
م = ـــــــــــــــــــــــــــــــــــــــ
          ظا(ط/2 - ط/ن)

                         ن نق²
نهـــــــــــــا ــــــــــــــــــــــــــــــــــــ = ∞/∞  كمية غير معينة
ن←∞          ظا(ط/2 - ط/ن)

لاحظ ان مدى الظل الى مالا نهاية .. وعندما نعوض بـ ن = ∞
فإن الزاوية تقترب جداً من 90 وهذه القيمة تقترب من الانهاية ..
نشتق كلاً من البسط والمقام على جدى ( حسب قاعدة لوبيتال)
((( لااااااااااااااحظ  .. الإشتقاق بالسبنةلـ ن  )))
النهاية بعد الإشتقاق تصبح :

                          نق²
نهـــــــــا ـــــــــــــــــــــــــــــــــــــــــــــــ
ن←∞        ط/ن² قا²(ط/2 - ط/ن)

لاحظ ان اشتقاق ظا(ط/2 - ط/ن) = مشتقة الزاوية × مشتقة الدالة نفسها

وهذه الصيغة تكافىء ( بعد التعديل )


             نق² ن² جتا²(ط/2 - ط/ن)
نهـــــــــا ـــــــــــــــــــــــــــــــــــــــــــــــ
ن←∞                 ط

ولكن جتا²(ط/2 - ط/ن) = جا²(ط/ن)         الزاوية المتممة لها ..


                نق² ن² جا²(ط/ن)
نهـــــــــا ـــــــــــــــــــــــــــــــــــــــــــــــ
ن←∞                 ط

نلاحظ ايضاً ان هذه النهاية = ∞/∞  (( جربها بنفسك، لكن بصيغة أخرى غير هذه ))
نشتق مرة أخرى كلاً من البسط والمقام على حدى .. ولكن قبل اجراء الإشتقاق
نضرب بسطاً ومقاماً فى  ن  حتى نستطيع حلها بقاعدة لوبيتال ..


                نق² ن³ [جا(ط/ن) ]²
نهـــــــــا ـــــــــــــــــــــــــــــــــــــــــــــــ
ن←∞                 ط ن

لاحظ البسط عبارة عن مشتقة الأول × الثانى + مشتقة الثانى فى الأول

                 3نق² ن² [جا(ط/ن) ]² + 2جا(ط/ن) × (-ط/ن²) جتا(ط/ن) نق² ن³
= نهـــــــــا ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
   ن←∞                                       ط


                     3نق² ن² [جا(ط/ن) ]² - جا(2ط/ن) × ط ن نق²
= نهـــــــــا ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
   ن←∞                                       ط

بالضرب بسطاً ومقاماً فى  ط/ن²     ... لماذا ؟؟


                     3نق² ط [جا(ط/ن) ]² - جا(2ط/ن) × (ط²/ن)  نق²
= نهـــــــــا ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
   ن←∞                                  (ط/ن)²

 لاحظ  عندما تسعى ن الى ∞  فإن   ط/ن  يسعى الى الصفر ، وبناء عليه :-
يكون : [جا(ط/ن) ]² / (ط/ن)² = 1          .. تابع

                              جا(2ط/ن) × (ط²/ن)  نق²
=  3نق² ط - نهـــــــــا ـــــــــــــــــــــــــــــــــــــــــــــــ
                  ن←∞             (ط/ن)²

نقوم بضرب النهاية الثانية بسطاً ومقاماً فى 2 .. لماذا ؟؟


                              2جا(2ط/ن) × (ط²/ن)  نق²
=  3نق² ط - نهـــــــــا ـــــــــــــــــــــــــــــــــــــــــــــــ
                  ن←∞        (2ط/ن) (ط/ن)

= 3ط نق² - 2ط نق²  = ط نق²

تابع القراءة

5 كيف نحسب جا18 بدون آلة حاسبة ؟

نستغل خاصية مهمة جداً فى حساب المثلثات، وهى ان :
جيب الزاوية = الجيب المتمم للزاوية المتممة

وايضاً نستطيع استعمال خاصية جا ضعف الزاوية،
وقانون مجموع زاويتين، او الفرق بينهما ... الخ

جا36 = جتا54

2جا18جتا18 = جتا(36+18)

2جا18جتا18 = جتا36 جتا18 - جا36 جا18

2جا18جتا18 = جتا36 جتا18 - 2جا18جتا18 جا18   بقسمة الطرفين على جتا18

2جا18 = جتا36 - 2جا²(18)    ولكن جتا36 = جتا2(18) = 1 - 2جا²(18)

2جا18 =  1 - 2جا²(18) - 2جا²(18)

2جا(18) =  1 - 4 جا²(18)           بترتيب الحدود نحصل على :

4جا²(18) + 2جا(18) -1 = 0      نفرض ان : جا18 = ص

4ص² + 2ص - 1 = 0         ( الحل بالقانون العام)

المميز = جذر( 4 + 16) = 2جذر5



           -2 ± 2جذر5                   -1± جذر5
ص = ـــــــــــــــــــــــــــــــــــ  = ــــــــــــــــــــــــــــــــــ
                  8                                 4

                      -1 + جذر5
اذاً  جا18 = ــــــــــــــــــــــــــــــــ
                           4

(( لاحظ ان الحل السالب مرفوض،، لأن جا موجبة فى الربع الأول ))

تابع القراءة

0 اثبت ان جتاس - جتاص = -2جا½(س+ص) جا½(س-ص)

نعلم من قانون مجموع زاويتين، والفرق بينهما الآتى : -


جتا[(س+ص) + (س-ص) ] = جتا(س+ص) جتا(س-ص) - جا(س+ص) جا(س-ص)         (1)


جتا [(س+ص) - (س-ص)] = جتا(س+ص) جتا(س-ص) + جا(س+ص) جا(س-ص)         (2)


ـــــــــــــــــــــــــــــــ بطرح  (2) من (1) ـــــــــــــــــــــــــــــــــــــــــــ


جتا2س - جتا2ص = -2 جا(س+ص) جا(س-ص)

(( وبوضع  س بدلاً من 2س ، ص بدلاً من 2ص للطرفين .. لأنها متطابقة ))


جتاس - جاص = -2جا½(س+ص) جا½(س-ص)


وهكذا حصلنا على المطلوب، اذا كنت تعلم لهذا القانون اثبات آخر، فأحضره لنا
حتى يستفيد منه الجميع .. تحياتى

تابع القراءة

2 اوجد نها(س←ط/4) [جتاس - جاس]/[س - ط/4]

                  جتاس - جاس
نهــــــــــــا ـــــــــــــــــــــــــــــــــ
س←ط/4         س - ط/4

عند التعويض بـ س = ط/4 تعطى كمية غير معينة

لاحظ ان جاس = متممة جتاس .. بمعنى
جاس = جتا(ط/2 - س )   وليس كما كتبت س - ط/2  لأ العكس هو اللى صحيح
طيب لو كتبناها  س - ط/2  يحصل حاجة ؟؟ طبعاً لا .. لماذا ؟؟
لأن جتا(-س) = جتاس  (( ارجو ان تكون هذه الخطوة واضحة ))


                      جتاس - جتا(س - ط/2 )
= نهــــــــــــا ـــــــــــــــــــــــــــــــــــــــــــــــــــــــ
   س←ط/4                س - ط/4


هناك قانون هام فى حساب المثلثات وهو يقتضى الآتى :

جتاس - جتاص = -2جا½(س+ص)جا½(س-ص)

وبناء عليه يكون :

جتاس - جتا(س - ط/2) = -2جا½(س+س -ط/2)جا½(س - س + ط/2)

= -2جا½(2س -ط/2)جا½( ط/2)

= -2جا(س - ط/4) جا(ط/4)     بالتعويض فى النهاية الأصلية

   
                -2جا(س - ط/4) جا(ط/4)
نهـــــــــــا ــــــــــــــــــــــــــــــــــــــــــــ
 س←ط/4           (س - ط/4)


                                  جا(س - ط/4)
= -2جا(ط/4) نهـــــــــــا ـــــــــــــــــــــــــــــــــ
                 س←ط/4        (س - ط/4)


                          جا(س - ط/4)              
ولكن نهــــــــــــــا ــــــــــــــــــــــــــــــــــ = 1     (( راجع نهاية الدوال المثلثية ))
       س←ط/4          (س - ط/4)

                                                                  جذر2
فيكون شكل النهاية الأخير = -2جا(ط/4) = -2 × ـــــــــــــــــ = - جذر2
                                                                    2


ملحوظة أخيرة : يمكن حل هذه النهاية بقاعدة لوبيتال
لكنها غير مسموح بها ( فى المدارس )

تابع القراءة

1 مبادى قواعد الإشتقاق فى الرياضيات، وقاعدة المتسلسلة

لو دققت فى الرسم جيداً ربما تفهم المعنى الهندسى للمشتقة الأولى

المشتقة معناها ايجاد ميل الدالة .. ولما كان ميل الدالة الأعلى من الدرجة غير
غير ثابت .. اوجدنا معدل تغير ص على معدل تغير س ..

لماذا ميل الدوال من الدرجة ما بعد الأولى غير ثابت ؟؟
لأنهم يشكلون منحينيات وليس خط مستقيم .. فهل المنحنى
خط مستقيم يميل ؟؟ ام انه يميل على جميع النقاط التى تقع
عليه ؟؟ اى ان كل نقطة .. او كل نقطتين قريبتين جدا جدا على
المنحنى لهما ميل خاص .. ولما كان ذلك كذلك افترضنا انهم نقطة
واحدة نظرا ً لأن الفرق بينهم يؤوول الى الصفر .

                                   معدل تغير ص        فرق الصادات عندما يؤوول الى الصفر
الميل = المشتقة الأولى = ــــــــــــــــــــــــــ = ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
                                   معدل تغير س        فرق السينات عندما يؤول الى الصفر


فإذا عوضنا فى رقم فى الدالة وليكن س  ستكون الأخرى س + هـ

حيث هـ الفرق بين س الثانية وس الأولى .. وهـ تؤول الى الصفر


              فرق الصادات            د( س + هـ )   -  د ( س )
الميل = ـــــــــــــــــــــــــــــــــ = ـــــــــــــــــــــــــــــــــــــــــــــــــ
             فرق السينات                            هـ

وبوضع هـ = 0  نظرا ً لأنها قيمة مهملة تؤول الى صفر

            د( س +0 )   -  د ( س )          د(س) - د (س)       0
الميل = ـــــــــــــــــــــــــــــــــــــــــــــــ  = ــــــــــــــــــــــــ = ـــــــ = كمية غير معينة
                           0                             0                   0


0/0 كمية غير معينة اى ان ناتج ( المشتقة الأولى ) لم يتعين .. فنلجأ الى حيلة أخرى
وهى ان نوجد قيمة هذا المقدار عندما هـ تقترب او تؤول الى الصفر .. ونسمى هذا
بمعدل التغير .



معدل التغير ( المشتقة الأولى )

                     د( س + هـ )   -  د ( س )
=  نهـــــــــــــــــا   ــــــــــــــــــــــــــــــــــــــــــــ
      هـ ← 0                    هـ


نفرض ان الدالة تقول د(س) = س²    فما قيمة دَََ(س) = ؟؟




                     د( س + هـ )   -  د ( س )
=  نهـــــــــــــــــا   ــــــــــــــــــــــــــــــــــــــــــــ
      هـ ← 0                    هـ

د ( س + هـ ) معناها شيل كل س فى الدالة وضع مكانها  س + هـ

مرة أخرى .. المسألة من جديد



                          ( س + هـ )²   -  س²
=  نهـــــــــــــــــا   ــــــــــــــــــــــــــــــــــــــــــــ   (( بتحليل المقام مربع كامل ))
      هـ ← 0                    هـ

                       س² + 2هـ س + هـ² - س²                        2هـ س + هـ²
= نهــــــــــــــــــا  ـــــــــــــــــــــــــــــــــــــــــــــ = نهــــــــا  ـــــــــــــــــــــــــــــــــــــــــ
     هـ ← 0                      هـ                      هـ ← 0                  هـ

                          هـ ( 2س + هـ )
= نهـــــــــــــا ــــــــــــــــــــــــــــــــــــــــــــــ  (( بعد اختزال العامل الصفرى هـ بسطا ً ومقاما ً ))
    هـ ← 0                   هـ


= نهـــــــــــــــــــا  2س + هـ    ولما كانت قيمة هـ مهملة وضعنها بصفر
      هـ ← 0


= 2س    اذا ً مشتقة  س²  = 2س


لكن انا اتحدث فى حالة تريد ان تطبق العام على الخاص .. بمعنى ان تضع مكان الأس ن

فتقول د(س) = س^ن    فهذا النوع من الإثبات اذا اوجدناه بمعدل التغير سيكون من الصعب
قليلا ً حيث ان قيمة الأس  ن مجهولة  .. لكن بعد معرفتنا بـ اللوغاريتم الطبيعى لط فكان الأمر
سهل ان نثبت ان مشتقة  س^ن    =  ن س^(ن-1)

وقد اثبت لك كيف نثبتها عن طريق أخذ اللوغاريتم الطبيعى للطرفين


د(س) = س^ن  


لط د(س) = لط س^ن

لط د(س) = ن لط (س)     (( حيث ن ثابت )) وبعد ان نشتق الطرفين بالنسبة لـ س


هذا الإثبات يجب ان تكون على معرفة جيدة باللوغاريتم الطبيعى وخواصه وطريقة اشتقاقه .

  دَ(س)         ن
ــــــــــــ  = ــــــــــــ
  د(س)        س

                ن  د (س)
دَ(س) = ـــــــــــــــــــــــــــــ    ولكن د(س) = س^ن
                    س

               ن س^ن
دَ(س) = ـــــــــــــــــــــــــــــ  = ن س^(ن-1)
                  س

تابع القراءة