اين انت .... » الرئيسية »
التفاضل والتكامل
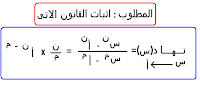
» اثبات قانون "4" فى التفاضل بقاعدة لوبيتال
اثبات قانون "4" فى التفاضل بقاعدة لوبيتال
الأحد، 16 أكتوبر 2011
التسميات:
التفاضل والتكامل
تنص قاعدة لوبيتال على انه اذا كانت الدالة على هذه
الصورة د(س) = ق(س)/ر(س) وكانت تعطى
كمية غير منعينة 0/0 او ∞/∞ فإننا نقوم بإشتقاق
البسط مرة، والمقام مرة ( كلاً منهم على حدى)
فإذا لم تتعين النهاية نشتق مرة أخرى .. وهكذا
الى ان يتعين الناتج .
س^ن - أ^ن ن نهـــــا ـــــــــــــ = ـــــــ × أ^ن-م س←أ س^م - أ^م م** ولكن لاحظ ان كلاً من أ ، م ، ن ثوابت
نقوم بإشتقاق البسط مرة، والمقام مرة .. فنحصل على الآتى :
ن س^(ن-1) نهـــــا ــــــــــــــــ س←أ م س^(م-1)لاحظ ان الاساسات متشابهة فنقوم بطرح الاسس ..
= نهــــا ن/م س^[ن-1 - (م-1) ] = نهـــان/م س^(ن-1 -م+1 ) س←أ س←أ
= نهـــــان/م س^(ن-م) وبوضع س = أ س←أ
ن
= ـــــ أ^(ن-م)
م
وهكذا حصلنا على المطلوب : للمزيد 








































3 التعليقات:
لو سمحتوا ممكن حد ينزل الاثبات بس من غير الأس في المقام نعتبره واحد بس
كيف يمكن أن تكون ن س^(ن-١)
=
س^ن -ا^ن
اعتبر ان أ^ن دي مش موجودة يعني = صفر ... طب ليه ؟؟ لأن أ و ن دول ثوابت ومشتقة الثوابت = صفر لأن مثلا لو د(س)=ص=٥^٢ يعني =٢٥ يبقا الدالة عبارة خط يقطع محور الصادات فال٢٥ وبيوازر السينات وساعتها مشتقته او فرق الصادات ÷ فرق السينات = صفر لأنه خط مستقيم فرق الصادات فيه بصفر فعسان كده واخدين قاعدة اي ثابت مستقته بصفر تمام ( حتي هوه قالك لاحظ ان أ و ن و م ثوابت) .. اتمني يكون الرد وصلك
إرسال تعليق