0 ما هى أساسيات التعامل مع محرك البحث wolfram alpha ؟

سأكتب أهم الوظائف الرياضية فقط وذلك لسهولة التعامل معها مستقبلاً .
موقع ولفرام الفا هو محرك بحث شيهر ليس مخصصاً فقط للرياضيات، ولكن
تقريباً لكافة المجالات العلمية، وسأتحدث هنا عن اهم الوظائف الرياضية
التى يتعامل معها الموقع .

الرابط الأساسى هو : http://www.wolframalpha.com/

عند فتح الرابط يظهر لك مربع محرك البحث، ومن خلاله فقط اذا
كتبت اى معلومة (ولتكن متعلقة بالرياضيات) ستجد معلومات
متوفرة عنها ===> مثال : اكتب فى محرك البحث :
the definition of prime numbers لتجد فى النتيجة result
معلومات بسيطة جداً عن الأعداد الأولية (طبعاً باللغة الإنجليزية)
ثم فى آخر المقال (للمزيد get more information) اذا ضغت عليها
ينقلك الى موضوع (الأعداد الأولية) الذى قد تناولة الموقع بشكل
أكثر موضوعية .

مثال آخر : اذا كتبت the definition of zeta function

ستجد معلومات (بسيطة جداً) متوفرة عن دالة زيتا الريمانية .. وهكذا

نتقل الى المحور الأساسى وهو كتاب الرموز والمعادلات الرياضية
فى مربع البحث :-

1) يمكنك كتابة اى عملية حسابية (اى كآلة حاسبة)
--------------------------------------------------------------------

♣ عملية الضرب يفصل بينهما اشارة * مثال 5 * 6
وعملية الجمع تستعمل الإشارة + والطرح تستعمل الإشارة -
والقسمة تستعمل الإشارة / .

♣ عدد مرفوع لأس : تستخدم الإشارة ^

مثال :   l                    5^2  ,    6^7
واذا اردت كتابة الجذر التربيعى فقط اكتب sqrt(x) 
مثال :  sqrt5

♣ التباديل : npa  مثال 5p3 
التوافيق : nca  مثال 5c3  وطبعاً توجد طرق أخرى للكتابة ..

2) نظرية الأعداد
---------------------

♣ تعميل عدد ما : لتعميل عدد ما _تحليله ما عليك سوى ان تكتب قبله كلمة factor
مثال : factor 105  لتجد انه اعطاك عوامل العدد 105 وايضاً قواسمه .

♣ القاسم المشترك الأكبر والمضاعف المشترك الأصغر :
لإيجاد القاسم المشترك الأكبر بن مجموعة من الأعداد نكتب :
gcd(a,b,c,d, ....)  l   مثال : gcd(105 , 15 , 27) لتجد ان النتيجة هى 3

لإيجاد المضاعف المشترك الأصغر لمجموعة من الأعداد نكتب :
lcd(a,b,c,d,....)   l  مثال lcd(105 , 15 , 27) لتجد ان الناتج هو 945

♣ الحصول على معلومات وقيم لبعض الدوال الخاصة :
مثل دالة زيتا :  zeta(2)  ,  zeta(x)   ..
او دالة phi (لأويلر)   phi(100) = 40   :مثال ... وهكذا

♣ للتحويل من اى نظام الى آخر نكتب كلمة base او  to base
مثال : l    3 to base 2  يعنى حول 3 من النظام العشرى الى النظام الثانى .
مثال آخر : l  11 base 2 to base 16  والتى تعنى حول 11 من النظام الثنائى
الى النظام السادس عشري hexadecimal .

♣ تمثيل الأعداد على خط الأعداد :
مثال : number line 2 , 5 , 6 , 8  وتعنى مثل على خط الأعداد هذه الأرقام ...
مثال آخر : number line x>1,x<5  وتعنى مثل على خط الأعداد العلاقة x>1
والعلاقة x < 5  .


3) الدوال والمتباينات وطريقة وحلها وطريقة تمثيلها .
------------------------------------------------------------------
♣ منعاً للخبطة والصداع بمجرد كتابتك لصغية معادلة او مبتاينة ما تظهر لك
(معظم وليس كل) المعلومات عن العبارة التى ادخلتها، ولكن ماذا لو كنا نريد
شىء محدد كرسم دالة مثلاً او متباينة ؟

كل ما فى الأمر تذكر فقط كلمة plot :

مثال : plot  x^2 + y^2 = 1   والتى هى عبارة عن معادلة دائرة الوحدة .
مثال آخر : plot  x^2 >=x والتى تعنى اننا نريد رسم المتباينة x² ≥ x
او بمعنى ادق منطقة الحل .

وبنفس الطريقة يمكنك رسم دالة فى فضاء ثلاثى الأبعاد :
مثل : plot x²+y²

ملحوظة : جرب ان تستبدل كلمة plot بـ graph (اعتقد لا فرق -- على العموم جرب)

لرسم علاقتين معاً او أكبر : كل الذى تسويه هو ان تضع كلمة and او فاصلة كهذه ,

مثال : plot x^2 and x^3   او تكتب هكذا  plot x^2 , x^3  كما يمكنك رسم دالة
مع متراجحة (متباينة) .. واشياء ومميزات أخرى كثيرة ستكتشفها بنفسك .

♣ حلول معادلة او متباينة :
لاحظ انه بمجرد وضعك للعلاقة فى محرك البحث يعطيك معلومات لا بأس بها عنها
ولكن ربما نحن نريد الحل فقط (ونسيبنا من وجع الدماغ ده كله) فقط نكتب كلمة
solve قبل العلاقة ، وكمثال على ذلك : solve x² - x + 4

♣ معرفة المجال والمدى :
فى حالة المجال نكتب قبل العلاقة domain of  وفى حالة المدى نكتب range of
مثال : domain of sqrt(x)    l   و  range of sqrt(x)   l


4) الجبر الخطى والمصفوفات :
-----------------------------------------
♣ المتجهات :  لتمثيل متجه نكتبه بين <>  مثال <3 , 4  , 1>
ولكن الأصح هو ان تضع قبله كامة vector
مثال : vector {1 , 2 , 3}   l  

♣ الضرب القياسى (النقطى) والضرب الإتجاهى :

مثال :  l       <1 , 4 , 7> dot <-1 , 5 , -4>     l
         l     <1 , 4 , 7> cross <-1 , 5 , -4>     l

الأول تعنى الضرب القياس لمتجهين والثانية الضرب الإتجاهى .

♣ كتابة المصفوفات والمحددات واجراء العمليات الجبرية عليها .

لكتابة المصفوفة بشكل سليم نضعها فى {} وكل صف فيها ايضاً نضعه فى {}

مثال :   l  {{1,2,5} , {7,-2,-1} , {0,4,5}}    l

يعنى عندنا مصفوفة 3 × 3 الصف الأول هو {1,2,5} و الثانى هو {7,-2,-1}
والثالث هو {0,4,5} .

ولكتابة محدد المصفوفة فقط نكتب قبلها كلمة det

 l      det {{1,2,5} , {7,-2,-1} , {0,4,5}}    l

ملحوظة : انسخ ما بين  |        |   وضعتها فقط منعاً لحدوث مشاكل فى الكتابة .

ولإيجاد معكوس المصفوفة نكتب قبلها كلمة inverse 

l    inverse {{1,2,5} , {7,-2,-1} , {0,4,5}}    l

ويمكنك اختصار الكلمة الى inv  او يمكنك الإستغناء عن هذا كلمة ونكتبها
بهذه الشكل :

l           {{1,2,5} , {7,-2,-1} , {0,4,5}}^-1   l

كما توجد أشياء أخرى كالرتبة والصفرية وغيرها ...

♣نأتى الى النقطة الأخيرة وهى يجوز لك ان تستعمل اشارات الجمع والطرح والضرب
فى المصفوفات ، ولكن لضرب مصفوفتين تعلم انه يجب ان يتحقق شرط أساسى
وهو ان عدد الأعمدة فى المصفوفة الأولى = عدد الصفوف فى المصفوفة الثانية .
ولضرب مصفوفتين نضع بينهما نقطة .

مثال :

l      {{1,2,5} , {7,-2,-1} , {0,4,5}}.{{4,1} , {-1,2} , {4,6}}   l

كما يمكنك اجراء العمليات على الصفوفات (مثل طريقة الحذف)

مثال :


l          row reduce {{1,2,5} , {7,-2,-1} , {0,4,5}}   l

♣ بحث الإستقلال الخطى :

مثال :

linear independence <1,2,5>, <7,-2,-1>, <0,4,5>     l


5) التفاضل والتكامل
-------------------------
♣ تكامل دالة : لتكامل دالة ما نكتب قبلها int
مثال : int x^2 dx  أو  int x^2 dx from x=0..1 
وتعنى التكامل المحدد من 0 الى 1 .

♣ لإشتقاق دالة بالنسبة لمتغير ما .

مثال :  d/dx x^2  والتى تعنى احسب المشتقة بالنسبة لـ x

ملحوظة : نفس الكلام ينطبق على المشتقة الجزئية .

مثال : d/dx x^2+y^2 والتى تعنى اوجد المشتقة الجزئية بالنسبة لـ x

♣ ايجاد المشقتة الثانية :

مثال :  the second derivative of cos(x)   l

 او يمكنك كتابتها بهذه الصورة d^2/dx^2 cos(x)

وهذا فالمشتقة الخامسة تكون هكذا :

the fifth derivative of cos(x)   l

♣ النهايات

مثال : lim sin(x)/x as x->0 

وتعنى ايجاد نهاية sinx/x عندما x تؤول للصفر .. اظن الأمر بسيط جداً ..
ولإيجاد النهاية عند اللانهاية نكتب : as x->inf  ولإيجاد النهاية على يمين
عدد معين (ليكن الواحد) نكتب as x->1+    l  واذا كنا نريد النهاية من
اليسار نكتب :  as x->1-        l

♣ متسلسلة تايلور :

مثال :  taylor series of sinx وتعنى ايجاد منشور تايلور لـ sinx

يمكنك ايضاً ان تحدد حول اى قيمة ؟

مثلاً : taylor series of lnx at x = 1

وتعنى منشور تايلور للدالة lnx حول x=1

♣ رمز المجموع (سيجما) ورمز حاصل الضرب .

مثال : sum n, n=1..100  او تكتب بهذه الطريقة sum n, n=1 to 100
او بهذه الطريقة : sigma n, b=1..100  ,تعنى بإختصار شديد حساب مجموع
الأعداد من 1 الى 100 والذى يساوى 5050

مثال الضرب : product 1 - 1/n , n=2..10  وتعنى حاصل الضرب من n=2 الى
n = 10  للضرب التالى :

l       (1 - 1/2)(1 - 1/3)(1 - 1/4) .... (1 - 1/10)   l

♣ لإيجاد النقاط الحرجة ونقاط الإنعطاف .

مثال على النقاط الحرجة : critical points of x^2 
مثال على نقاط الإنعطاف : inflection points of x^4-3x^2+x

♣ التحويلات التكاملية :
مثال على تحويل فورير : foureir transform of e^(-x^2)
مثال لعى تحويل لابلاس : LT cosx

نعلم ان تحويل لابلاس لـ cosx هو s/(s²+1)  l
ولكن ماذا لو كنا نبحث عن تحويل لابلاس العكسى ؟

نكتب الآتى : inv LT s/(s^2+1)   l  يحولنا مباشرة ً الى cosx

6) الإنشاءات الهندسية
------------------------------
فى حقيقة الأمرة هذا الموضوع طويل، نظراً لتعدد انواع الهندسة الكثيرة
فى الرياضيات لذلك فقط يكفى ان تتعلم الأساسيات كرسم دائرة او مربع
او مثلث بطريقة معينة ما .

♣ رسم مثلث بمعلومية أضلاعه .

مثال :  l      3,4,5 triangle   وتعنى ارسم المثلث الذى أضلاعه 3 , 4 , 5

♣ رسم دائرة ، وبقية الأشكال بنفس الطريقة ..

مثال : مثال : circle,r=5  وتعنى ارسم الدائرة التى طول نصف قطرها = 5

كما تلاحظ الأمور بسيطة جداً، لك فقط ان تكتب اسم الشكل ثم فاصلة وتكتب
مميزات هذا الشكل (مثلاً الذى يميز كرة عن أحرى هو نصف القطر فقط) لذلا
فإن اردنا ان نرسم كرة نصف قطرها 8  نكتب الآتى : sphere,r=8

مثال آخر : cylinder,r=3,h=5 والذى يعنى اسطوانة نصف قطر قاعدتها 3 وارتفاعها 5 .

مثال : rectangle,height=8,width=3  وتعنى ارسم المستطيل الذى طوله 8 وعرضه 3

♣ التحويل من القياس الستينى الى الدائرى والعكسى .

مثال : l          30 deg to rad 

وتعنى حول قياس الزاوية 30 بالتقدير الدائرى .

اذا قولنا  l   pi/6 rad  to  deg

وتعنى حول من التقدير الدائرى الى القياس الستينى (بالدرجات)

♣ التحويلات القطبية

مثال على الإحداثيات القبطية :  l        (1,2) in polar form

وتعنى حول l (1,2) الى الإحداثيات القطبية

6) الإحصاء والإحتمالات     (سأذكر أهم الوظائف فقط)
----------------------------
♣ حساب الوسط الحسابى لمجموعة من الأعداد .
مثال : mean {3, 5,7,11,6,18}  = 25/3
♣ حساب المتوسط الحسابى :
مثال : median {1 , 3 , 5 , 9} = 4
♣حساب الوسط الهندسى :
مثال : geometric mean {8 , 6 , 12 , 14 , 5}  ≈  8.34
♣ التباين والإنحراف المعيارى
مثال : variance {7, 4, 8,9} = 14/3
standard deviation {7, 4, 8,9} = sqrt(14/3)   l
♣ رسم منحنى التوزيع الطبيعى بمعرفة الوسط الحساب والإنحراب المعيارى
مثال : normal distribution, mean=0, sd=2

مثا آخر : P[1<X<2] for normal distribution Mean=0,sd=1

mean = الوسط الحسابى ،  sd = الإنحراف المعيارى
♣ توزيع ثنائى الحدين :

مثال : binomial distribution n=5, p=0.3

حيث n = عدد المرات  و p = احتمال النجاح

مثال آخر : prob x>5 for x binomial with n=14 and p=.36


°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°

كانت هذه أهم الأشياء، والأكثر استعمالاً فى الرياضيات، ولهذا
فيمكنك التوسع اكثر من ذلك ان أحببت للبحث عن مواضيع
أخرى تهتمك .

تابع القراءة

0 احسب l (1-4/1^2) (1-4/3^2) (1-4/5^2) .... (1-4/195^2) (1-4/197^2)(1-4/199^2)‏

ليكن لدينا دالة فى المتغير a حيث  a = 1,3,5,7,...,199

f(a) = 1 - 4/a² = (1 + 2/a) ( 1 - 2/a)  = [(a+2)/a] [(a-2)/a] = (a-2)(a+2)/a²   l

الآن بحث عن سير عمل هذه الحدود (يعنى بالتعوض مرة عن a = 1  تعطينا
الحد الأول ثم نعوض a = 3 تعطينا الحد الثالث ... وهكذا)

ليتكون لدينا الشكل الآتى فى الضرب .

l  (-1×3)/1² . (1×5)/3² . (3×7)/5² . (5×9)/7² ... (195×199)/197² . (197×201)/199²

مما سبق نكتشف ان هناك اختصارات كثيرة جداً تتلخص فى انه (مثلاً)
لكى نختصر 3² التى فى المقام يكفى ايجاد 3 مضروبة فى 3 (مكررة يعنى)
فى البسط وهذا موجود ويطبق على جميع الحدود بإستثناء الحد الأخير لا
تطبق عليه القاعدة بشكل كامل فهو يبقى على a+2  وايضاً فى المقام يبقى
على a فقط (يمكن ملاحظة ذلك من خلال التجربة)

وايضاً نلاحظ ان هناك سالب واحد (اذاً المقدار سالب)

وبناء عليه فإن حاصل الضرب هو :   P = -(199+2)/199 = -201/199

والتى تساوى بالتقريب :  P ≈ -1.01

---------------------------------------------------------------------------------------------
والآن لتكن الحدود عددها
لانهاية بحيث ان الترتيب فى المقامات فردى كما هو واضح، كل ما
نفعله هو نوجد النهاية للدالة الآتية .

lim(a→∞)  - (a+2)/a  = -1

تساوى  -1  لأن درجة البسط = درجة المقام
اذاً مباشرة ً النهاية = معامل a الذى فى البسط
على معامل a الذى فى المقام يعنى تساوى 1/1 = 1
ثم ضربنا النهاية فى سالب واحد كما حددنا لأن الحد الأول
منها سالب .

وبناء عليه اذا كان الضرب السابق يؤول الى اللانهاية فإن
قيمته تؤول الى -1   .

l                                    (1-4/1^2) (1-4/3^2) (1-4/5^2) ........ = -1‏

--------------------------------------------------------------------------------------------------

وجدت ان موقع ولفرام الفا لا يستحمل سوى عدد معين من العمليات
الحسابية، لذلك وضعت الناتج فى آلة حاسبة مخصصة للعمليات الحسابية
الكبيرة ووضعت فيها :

(1-4/1^2)*(1-4/3^2)*(1-4/5^2)*(1-4/7^2)*(1-4/9^2)*(1-4/11^2)*(1-4/13^2)*(1-  4/15^2)*(1-4/17^2)*(1-4/19^2)*(1-4/21^2)*(1-4/23^2)*(1-4/25^2)*(1-4/27^2)*(1-  4/29^2)*(1-4/31^2)*(1-4/33^2)*(1-4/35^2)*(1-4/37^2)*(1-4/39^2)*(1-4/41^2)*(1-  4/43^2)*(1-4/45^2)*(1-4/47^2)*(1-4/49^2)*(1-4/51^2)*(1-4/53^2)*(1-4/55^2)*(1-  4/57^2)*(1-4/59^2)*(1-4/61^2)*(1-4/63^2)*(1-4/65^2)*(1-4/67^2)*(1-4/69^2)*(1-4/71^2)*(1-4/73^2)*(1-4/75^2)*(1-4/77^2)*(1-4/79^2)*(1-4/81^2)*(1-4/83^2)*(1-4/85^2)*(1-4/87^2)*(1-4/89^2)*(1-4/91^2)*(1-4/93^2)*(1-4/95^2)*(1-4/97^2)*(1-4/99^2)*(1-4/101^2)*(1-4/103^2)*(1-4/105^2)*(1-4/107^2)*(1-4/109^2)*(1-4/111^2)*(1-4/113^2)*(1-4/115^2)*(1-4/117^2)*(1-4/119^2)*(1-4/121^2)*(1-4/123^2)*(1-4/125^2)*(1-4/127^2)*(1-4/129^2)*(1-4/131^2)*(1-4/133^2)*(1-4/135^2)*(1-4/137^2)*(1-4/139^2)*(1-4/141^2)*(1-4/143^2)*(1-4/145^2)*(1-4/147^2)*(1-4/149^2)*(1-4/151^2)*(1-4/153^2)*(1-4/155^2)*(1-4/157^2)*(1-4/159^2)*(1-4/161^2)*(1-4/163^2)*(1-4/165^2)*(1-4/167^2)*(1-4/169^2)*(1-4/171^2)*(1-4/173^2)*(1-4/175^2)*(1-4/177^2)*(1-4/179^2)*(1-4/181^2)*(1-4/183^2)*(1-4/185^2)*(1-4/187^2)*(1-4/189^2)*(1-4/191^2)*(1-4/193^2)*(1-4/195^2)*(1-4/197^2)*(1-4/199^2)


فكان الناتج بالتقريب    l                                      ≈ -1,01

وهو نفس الناتج الذى توصلت اليه .   (من هذا الموقع)

-------------------------------------------------------------------------------------------
يمكن وضع حاصل الضرب السابق فى موقع ولفرام الفا كما هو مبين على
هذا الرابط .

تابع القراءة

2 اوجد : lim(x→∞) xlnx - xln(x-1) l

بالتعويض المباشرة تعطى مالانهاية - مالانهاية  (كمية غير معينة)
ولكن يمكن وضع النهاية فى صورة أخرى (ومن خصائص اللوغاريتمات)

lim(x→∞) xlnx - xln(x-1)  ==> lim(x→∞) x [lnx - ln(x-1)]  l

ولتحويلها الى نهاية (فى صورة كسر) نفرض أن : x = 1/y
ومنها  y = 1/x  وعندما x تؤول الى مالانهاية فإن y تؤول الى الصفر .

lim(y→0)  [ln(1/y) - ln(1/y -1)]/y    وبتوحيد المقامات

L = lim(y→0) [ln(1/y) - ln((1-y)/y)]/y

بإستعمال بعض خصائص اللوغاريتمات البسيطة ...

L = lim(y→0) [-lny - ln(1-y) + lny)]/y

L = lim(y→0) - ln(1-y)/y

بعد التعويض بـ y = 0  نجد ان النهاية = 0/0 وهنا يجوز
استعمال قاعدة لوبيتال عن طريق اشتقاق البسط مرة
والمقام مرة (كلاً منهم على حدى)
-------------------------------------------------------------------------- للتأكد من ان حلك سليم :-

lim(x→∞) xlnx - xln(x-1)         l

ما عليك سوى رسم الدالة فى اى برنامج متخصص فى رسم الدوال
او مباشرة ً ترسمها فى موقع ولفرام الفا، ومن خلال الرسم يتضح
(اذا نظرنا على محور x متجه نحو اللانهاية) نجد ان الدالة تقترب من
قيمة معينة وهى 1 .

وكان فى الإمكان حل النهاية عن طريق متسلسلات النشر
ايضاً يمكنك حلها بالطريقة الآتية :

L = lim(x→∞) xlnx - xln(x-1) ==> lim(x→∞) x[lnx - ln(x-1)]   l

L =  lim(x→∞) xln[x/(x-1)]    l

نفرض أن : x/(x-1) = y  وعندما x تؤول الى مالانهاية فإن y تؤول الى الواحد
ولكن هذا يتطلب منا ايجاد x بدلالة y  .

x/(x-1) = y   ==> x = y(x-1)  ==> x = xy - y

اذاً :   xy - x = y   بأخذ x عامل مشترك ..

x(y-1) = y   ومنها   x = y/(y-1)   l   بالتعويض ... ويجب ان نتوخى الحذر
هنا ان النهاية ستحول الى دالة فى المتغير y بدلاً من x واننا برهنا على ان
اذا كانت x تؤول الى مالانهاية فإن y تؤول حتماً الى الواحد .

L =  lim(x→∞) xln[x/(x-1)]    l   بالتعويض ...

L =  lim(y→1) y/(y-1) * lny    l  

L =lim(y→1)  lny/(y-1)  *  lim(y→1)  y

النهاية الثانية بكل تأكيد ستكون 1 (والواحد لا يؤثر فى الضرب)

L =lim(y→1)  lny/(y-1)     l

عند التعويض بـ y = 1  تعطى كمية غير معينة 0/0

الذى اعرفه اننا يمكننا نشر lny بمنشور تايلور ومن ثم القسمة على y-1
فتعطى مباشرة ً 1 (وهذا ما سأبينه)

الطريقة الثانية : عن طريق قاعدة لوبيتال بإشتقاق البسط مرة والمقام مرة
كلاً منهم على حدى .

مشتقة البسط  هى مشتقة lny  وتساوى  l               1/y
مشتقة المقام هى مشتقة y-1  وتساوى    1

وبناء عليه تتحول النهاية الى :  L = lim(y→1) 1/y = 1

الطريقة الثانية عن طريق متسلسلات النشر .

lny = (y-1) - (y-1)²/2! + (y-1)³/3! -  ...     l

بقسمة الطرفين على y - 1

lny/(y-1) = 1 - (y-1)/2! + (y-1)²/3! - ... l

عندما y تؤول الى 1 فإن y - 1  تؤول للصفر حتماً
وبالتالى نجد ان جميع هذه الحدود صفراً فيما عدا طبعا ً الحد المطلق 1

اذاً :   L = 1‏

مشتقة المقام هى مشتقة y وتساوى 1

نفرض أن البسط f(y) = ln(1-y)   l

اذاً : f'(x) = -1/(1-y)  ll  بالتعويض فى النهاية ..

L = lim(y→0) - [-1]/(1-y)   l  وبالتعويض المباشر عن y = 0

نصل الى ان :          L = 1‏

تابع القراءة

0 برهن أن : ق.م.أ(أ^ن ، ب^ن) = [ق.م.أ(أ،ب)]^ن

نفرض أن : ق.م.أ (أ^ن ، ب^ن) = د1

اذاً : أ^ن = م1 د1     ،  ب^ن = م2 د1  حيث (م1 ، م2) = 1

ق.م.أ (أ ، ب) = د2

اذاً : أ = م3 د2   ،  ب = م4 د2        حيث (م3 ، م4) = 1

مما سبق نستنتج ما يلى :

م1 د1 = (م3 د2)^ن         ===>  1

م2 د1 = (م4 د2 )^ن        ===>  2

بضرب 1 ، 2

م1 م2 (د1)² = (م3 × م4)^ن × (د2)^2ن

وبقسمة الطرفين على م1 م2

              (م3 × م4)^ن × (د2)^2ن
(د1)² = ـــــــــــــــــــــــــــــــــــــــــــــــ     ====> (3)
                        م1 م2

بقسمة 1 على 2 فنحصل على :

    م1           (م3)^ن    
ــــــــــــــ = ـــــــــــــــــــــ
    م2           (م4)^ن

م1 × (م4)^ن = م2 (م3)^ن                ====> (4)

الآن طرفى المعادلة يقبل القسمة على م2 ولكن (م1 ، م2) = 1
اذاً (م4)^ن يقبل القسمة على م2 وبناء عليه يوجد عدد صحيح ك1
بحيث :

(م4)^ن = ك1 م2

بنفس الطريقة طرفى المعادلة يقبل القسمة على م1  اذاً

(م3)^ن = ك2 م1

ولكن : (م3 ، م4) = 1      (اوليان فيما بينهما - هذا هو القصد)

اذاً : (ك1 ، ك2) = 1     بالتعويض فى معادلة (4)

م1 × ك1 × م2 = م2 × ك2 × م1

اذاً : ك1 = ك2 = 1   لأن (م3 ، م4) = 1

وبناء عليه : (م4)^ن = م2

               (م3)^ن = م1

اذاً :  (م3 × م4)^ن = م1 × م2   بالعودة الى معادلة (3)

              (م3 × م4)^ن × (د2)^2ن
(د1)² = ـــــــــــــــــــــــــــــــــــــــــــــــ
                        م1 م2


اذاً : (د1)² = (د2)^2ن  ومنها د1 = (د2)^ن


اى أن :   (أ^ن ، ب^ن) =(أ،ب)^ن      #



مثال : ق.م.أ (196 ، 2401) = ق.م.أ [(14)² ، (49)²] = ق.م.أ (14 ، 49)² = (7)² = 49

وفى حقيقة الأمر كان يمكن اثبات ما سبق بطريقة أبسط من ذلك نفرض أن :

ق.م.أ (أ ، ب) = د     وبناء عليه فإنه يوجد عددان صحيحان م1 ، م1 بحيث ق.م.أ (م1 ، م2) = 1

تحقق : أ = م1 د     ،  ب = م2 د  

اذاً : أ^ن = م1^ن د^ن       ،  ب^ن = م2^ن د^ن

ق.م.أ (م1 ، م2) = 1  <===> ق.م.أ (م1^ن ، م2^ن) = 1

وبناء عليه فإن القاسم المشترك الأكبر بين أ^ن ، ب^ن هو د^ن  (انتهى البرهان البسيط)

تابع القراءة

1 برهن على انه اذا كان l (n-1)! + 1 يقسم على n فإن n عدد أولى

سأبرهن لك العبارة بطريقة سهلة :

ليكن n عدد طبيعى، نعلم ان جميع الأعداد الطبيعية اما ان تكون عدد
أولى او ليست عدد أولى (بمعنى آخر مجموعة الأعداد الأولية اتحاد
مجموعة الأعداد المؤلفة تعطى مباشرةً مجموعة الأعداد الطبيعية)

لذا فإن اجزمنا ان n عدد طبيعى (وهذا حقيقى لأننا نتعامل مع مضاريب
أعداد طبيعية) فإن لم يكن n عدد مؤلف فهو عدد أولى .

البرهان بالتناقض : ليكن n عدد مؤلف  <===> n = ab

حيث a , b أعداد طبيعية أكبر من الواحد واقل من n

    l                      1 >  a , b >  n                  l

اذاً : l     (n-1)!    l  يقبل القسمة على a , b  معاً اى انه يقبل
القسمة n ، ولهذا السبب فإن :   l        (n-1)! + 1  لا تقبل القسمة
على n ، وهذا تناقض أن العبارة تقبل القسمة على n اذاً n عدد أولى .

مثال :   l             [(5 - 1)! + 1]/5 = 5             l

ملحوظة أخيرة : وهذا البرهان يؤكد عكس مبرهنة ويلسون، او كما
يسميها البعض (مبرهنة ابن الهيثم - ويلسون) من اجل n عدد أولى
فإن :

l              (n - 1)! ≡ -1  (mod n)          l‏

تابع القراءة

0 أوجد هذا العدد المكون من اربعة ارقام

عدد مكون من أربعة أرقام يقع بين العددين 3000 و4000 مجموع أرقام العدد هو 21
وحاصل ضرب الآلآف والآحاد هو 24 ورقم المئات يقل 2 عن رقم العشرات فما هو هذا العدد؟

س ، ص ، ع ، د ارقام الآحاد والعشرات والمئات والألوف على التوالى ...

س+ص+ع+د = 21     ===>  (1)

س×د = 24               ===>  (2)

ص - ع = 2               ===>  (3)

من معادلة (3)  ص = ع+2  بالتعويض فى معادلة (1)

س+ع+2+ع+د = 21  ومنها س+2ع+د = 19         ===> (4)

                                 24
من (2)  نجد أن : س = ـــــــــــــ
                                 د

لابد ان تكون د  من قواسم العدد 24 ، ولكن لاحظ :

س،ص،ع،د ∈ {0 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9}

وهذا يدلنا (مثلاً) على ان د لا يمكن ان تكون 1

لأنه اذا كانت د=1 فإن : س = 24

الآن : عندما  د = 3     فإن    س = 8
       عندما  د = 4     فإن    س = 6
       عندما  د = 6     فإن    س = 4
       عندما  د = 8     فإن    س = 3

الذى يحدد اى الحلول السابقة صحيحة هى معادلة (4)  .. بالتعويض

س+2ع+د = 19         ===> (4)

فيمكنك التعويض بالحل الأول : د = 3   عندما  س = 8

8 + 2ع + 3 = 19    اذاً  2ع = 19 - 11 = 8  ومنها ع = 4

عندما  د = 4     فإن    س = 6

6 + 2ع + 4 = 19    ومنها  ع = 4.5   وهذا مرفوض .

عندما  د = 6     فإن    س = 4

ايضاً هذا الحل مرفوض ...

عندما  د = 8     فإن    س = 3

هذا الحل مكرر  ..

اذاً :   س = 8  عندما  ع = 4     ،   د = 3

بالتعويض فى المعادلة : ص = ع+2

ص = 4 + 2 = 6

اذاً العدد الوحيد هو :  3468

تابع القراءة

0 كيفية ايجاد مساحة الدائرة الداخلة للمثلث ؟

لدينا في المثلث نقطة تقاطع المنصفات هي مركز الدائرة التي داخل المثلث
السؤال هو كيف نحسب مساحة هذه الدائرة؟ هل يوجد قانون اوشيء ما يساعد في حساب مساحتها؟
علما ان نصف قطرها مجهول، والمعلوم هو اطوال المثلث .

لك فقط ان تعلم قاعدة هيرون لإيجاد مساحة
المثلث بدلالة أطوال أضلاعه، فإذا كانت أطوال أضلاع المثلث (اى مثلث)
هى a , b , c  فإن مساحته هى : A = sqrt[s(s-a)(s-b)(s-c)]  l
حيث s = (a+b+b)/2  أو بإختصار s هى نصف محيط المثلث، .
(اثبات مفصل لقاعدة هيرون)

ننتقل الآن الى سؤالنا : فكما أنك قلت ان الدائرة الداخلة للمثلث مركزها هو
نقطة تلاقى منصفات هذا المثلث، فإنه ايضاً من الضرورى ان تعلم ان نفس هذه
النقطة (مركز الدائرة) هى نقطة تلاقة انصاف أقطار الدائرة (حقيقة)، ومن ضمن
هذه الأنصاف اقطار التى تكون عمودى على المماس (المماسات هنا أضلاع المثلث)

نظرية : نصف القطر عمود على المماس .

فكرة الحل بسيطة جداً وهى ننا لو علمنا نصف قطر الدائرة لأوجدنا مساحتها .
الآن نعلم ان مساحة المثلث (بقاعدة هيرون) هى :
                                    A = sqrt[s(s-a)(s-b)(s-c)]  l

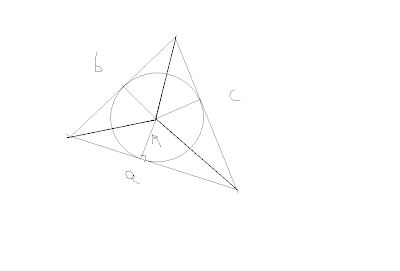
ولكن يمكن ايجاد مساحة المثلث بطريقة أخرى (او كام  هو موضح بالرسم)

مساحة المثلث = مساحة ثلاث مثلثات جميع ارتفاعتها (نصف قطر الدائرة)

مساحة المثلث = ½ القاعدة × الإرتفاع .

والآن بعد تقسيم المثلث (المحيط بالدائرة) الى ثلاث مثلثات نستطيع ان نوجد A
بطريقة أخرى وهى :

A = ½ar + ½br + ½cr = r(a+b+c)/2 = rs

اذاً : rs =  sqrt[s(s-a)(s-b)(s-c)]  l  بتربيع الطرفين ..

r²s² = s(s-a)(s-b)(s-c)  l   بقسمة الطرفين على s²

r² = (s-a)(s-b)(s-c)/s    بضرب الطرفين فى pi  (النسبة التقريبية)

pi r² = pi(s-a)(s-b)(s-c)/s

مثال : اذا كانت أضلاع المثلث هى : 9 , 7 , 5

s = (5+7+9)/2 = 10.5   وبالتالى فإن :

Area of circle = pi (10.5 - 5)(10.5 - 7)(10.5 - 9)/10.5 = 11pi/4 ≈ 8.64‏

تابع القراءة

1 أوجد عدد الرجال والنساء والأطفال ؟

في حفلة عشاء لدينا اناس يتكوّنون من رجال و نساء و اطفال عددهم 12 وضع لهم 12 من الخبز
المعطيات:
ياكل كل طفل ربع خبزة
تأكل كل المرأة 1.5 خبزة
يأكل كل رجل خبزتان
السؤال:
كم عدد الرجال و النساء و الاطفال في هذا الحفل
( يجب ان يكون الجواب مرفوق بالطريقة)

عدد الرجال = س ، عدد النساء = ص  ، عدد الأطفال = ع

س+ص+ع = 12              =====> (1)

2س+1.5ص+0.25ع = 12   =====> (2)     × -4

-8س-6ص-ع = -48   بجمعها مع (1)

-7س - 5ص = -36                          × -1

7س+5ص = 36     لاحظ ق.م.أ (7 ، 5) = 1 وهى تقسم 36

الآن نوجد القسم المشترك الأكبر بين 7 ، 5 بطريقة القسمة الخوارزمية .

7 = 1(5) + 2        ====>   2 = 7 - 1(5)          *

5 = 2(2) + 1        ====>   1 = 5 - 2(2)          **

بالتعويض من * فى **

1 = 5 - 2[7 - 1(5)] = 5 - 2(7) + 2(5) = -2(7) + 3(5)

الآن عندك : -2(7) + 3(5) = 1    بضرب الطرفين فى 36

7(-72) + 5(108) = 36    اذاً  س0 = -72   ،  ص0 = 108

لا تندهش كثيراً اعلم ان كلا من س ، ص ، ع يجب ان تكون محصورة
فى المجموعة {1 ، 2 ، 3 ، ..... ، 12} ولكن هذه قيم ابتدائية صحيحة
ننتقى منها فقط الحلول الطبيعية .

من خلال الحل الإبتدائى الذى توصلنا اليه نستطيع ان نكتب الحل العام بهذه
الطريقة (راجع طريقة حل المعادلات الديفونتية)

                         5          
س = س0 + ــــــــــــــــــــــــ ن = -72 + 5ن
                ق.م.أ (7 ، 5)

                        7
ص = ص0 - ــــــــــــــــــــــــــ ن = 108 - 7ن
               ق.م.أ (7 ، 5)

حيث ن عدداً طبيعياً .. ولآن نبحث عن كل الحلول الطبيعية لـ س، ص بحيث ان
كلاً منهم بالتأكيد اكبر من الواحد الصحيح واقل من 12 .

الحالة الأولى : نضع ن = 1   نجد أن : س = -67  ، ص = 101

      ((وكل هذه حلول مرفوضة))

وحتى لا اظل اعيد التجربة مرات عديدة استطيع ان افيدك فى أن الحل الوحيد
الطبيعى لـ س ، ص هو {(3 ، 3)}  بالتعويض فى (1)

س+ص+ع = 12              =====> (1)

3+3+ع = 12   ومنها  ع = 6

اذاً الحل الوحيد هو : ح = {(3 ، 3 ، 6)}

عدد الرجال = 3

عدد النساء = 3

عدد الأطفال = 6

---------------------------------------------------------------------------------------------------
طريقة أخرى للحل  (لكنها تحتاج الى ترتيب فى التفكير) عن طريق ترشيح
مجموعة او عدة مجموعات معينة تحقق تلك الشروط من عدد المجموعات
الكلى، الآن اقل عدد يمكن أن تأخذ فئة من الفئات الثلاث هو 1 وأكبر عدد
هو 10 وهو  {1 ، 1 ، 10} ويعتبر هذا الحل من اكبر الحلول الممكنة لوجود
العدد 10 فيه، الآن نجد فى هذا الحل عنصرين مكررين وهما (1 ، 1) لذا
فإن عدد المجموعات الممكنة هو 3 ل 2 = 3 مجموعات وهم (حسب الترتيب)
س ، ص ، ع  ...

{(1 , 1 , 10)} , {(1 , 10 , 1)} , {(10 , 1 , 1)} جميع هذه الحلول تحقق

المعادلة الأولى فقط : س+ص+ع = 12              =====> (1)

لنختبر هل هى تحقق المعادلة الثانية ؟

عوض بالحل : (1 , 1 , 10) فى المعادلة : 2س+1.5ص+0.25ع

2(1) + 1.5(1) + 0.25(10) = 6   اذاً ليس حلاً .. وهكذا عوض بالحلين
الآخرين تجد نفس المشكلة قد تكونت لديك .

والآن نركز على العدد 9 : {1 , 2 , 9}  اعتقد ان هذا تصور معقول، ولكن هذه
المجموعة تكرر بعدد 3! = 6  مجموعات ، وهم حسب الترتيب التالى :

{(1 , 2 , 9)} , {(1 , 9 , 2)} , {(2 , 1 , 9)} , {(2 , 9 , 1)} ,
{(9 , 1 , 2)} , {(9 , 2 , 1)} والآن اريدك ان تفهمنى بشكل سريع كل المجموعات
التى اضعها تحقق المعادلة الأولى (لأن عدد العناصر فيها = 12)

نأخذ كل حل من الحلول السابق ونعوض فى المعادلة الثانية (جربهم بنفسك)
نظراً لأن الوقت لم يسعنى هنا لأكتب خطوات مكررة لا داعى من ذكرها، فقط
لك ان تعلم ان الحلول السابق لا تحقق المعادلة الثانية (من خلال التجربة)

نظل هكذا ... العدد 8  ... ثم العدد 7  ... ثم العدد 6   (وهنا نجد ان حل ما قد تحقق)

الآن : المجموعات المولدة هى :  {1 , 5 , 6}  و {2 , 4 , 6} و {3 , 3 , 6}
كل مجموعة تولد عدد مجموعات عددها 3! = 6  كما اسلفنا وفعلنا فى المجموعات
السابقة لتجد ان جميعهم ليسوا حلاً للمعادلة الثانية الا المجموعة الاخيرة فهى
تحقق المعادلة الأولى والثانية معاً (بنفس ترتيبها)  اذاً {(3 , 3 , 6)} حلاً لهذا النظام .

ولكى تثبت وحدانيته عليك بتجربة باقى المجموعات ....

تابع القراءة

0 برهن على ان العدد (n^(p+1 و العدد (n^(p+5 آحادهما مشترك

لمعرفة رقم الآحاد لأى عدد نقسمه على 10 ، وبفرض أن آحاد العدد الأصغر
هو a  ... اذاً  n^(p+1) ≡ a (mod10)   l بضرب الطرفين فى n^4

n^(p+5) ≡ a n^4 (mod10)   l

اذاً يجب البرهنة على أن : a n^4 ≡ a (mod10)  l   (سأحاول ان اكمل هذا البرهان الناقص)...
------------------------------------------------------------------------------------------------------
سآتى الى النقطة الثانية (والتى لفتَّ نظرى اليها) يكون للعددين نفس رقم
الآحاد اذا كان الفرق بينهما عدد يقبل القسمة على 10 وهذا أمر جيد .

E = n^(p+5) - n^(p+1) = n^(p+1) [n^4 - 1]    l

حقيقية : يقبل عدد ما القسمة على 10 اذا كان يقبل القسمة على 2 ، 5 معاً .

الآن اذا كانت n عدداً زوجياً فإنه بالتأكيد يقبل القسمة على 2 اما اذا كانت n عدداً
فردياً فإنه يمكن وضع n على الصورة  n = 2k+1  حيث k عدد طبيعى .. ولكن دعنا
من هذا كله حيث انى سأعتمد على الحقيقة التى تقول ان : فردى × فردى = فردى
وبناء عليه فردى اس اى عدد طبيعى هو عدد فردى (يمكنك برهنتها والبرهان سهل)

اذاً n^4 - 1 = 2u   حيث م عدد طبيعى (اى انى اقصد انها عدد زوجى)

لأنه اذا كانت n^4 عدداً فردياً، فإنك تستطيع ان تعتمد على المعلومة فردى - فردى = زوجى .

هكذا تكون اول واهم خطوة انتهت وهى ان العدد يقبل القسمة على 2 من اجل ن عدداً طبيعياً .

ننتقل الى الخطوة التالية لها، وسأفرض أن p+1 = m   (حتى تكون واضحة لا اكثر)

E = n^m . [n^4 - 1]     l

من اجل n من مضاعفات العدد 5  (انتهى البرهان)

من اجل n ليست من مضاعفات العدد 5 اذاً يستحيل ان يقبل العدد n^m القسمة على 5
لماذاً ؟ لأنه اذا كانت n لسيت من مضاعفات العدد 5 اذاً فإن عواملها الأولية لا تحوى على
العدد 5 نفسه، وبناء عليه مهما رفعته لأس طبيعى فلن تحصل على مضاعفات للعدد 5 .
اذاً حتى نكمل البران عن آخره يجب ان نبرهن على ان n^4 - 1  تقبل القسمة على 5 من اجل
n عدداً طبيعياً ليس من مضاعفات العدد 5 .

جميع الأعداد الطبيعية التى ليست من مضاعفات العدد 5 تكون على احدى الصور الآتية :

5k+1   ,  5k+2   , 5k+3  , 5k+4   حيث k عدداً طبيعياً .

وحتى يكون الحل يسير نبدأ بنشر مفكوك ذات الحدين التالى :

l                       (x+a)^4 = x^4 + 4ax³ + 6a²x² + 4a³x + a^4

بوضع x = 5k  للطرفين ...

l       (5k+a)^4 = (5k)^4 + 4a(5k)³ + 6a²(5k)² + 4a³(5k) + a^4

الآن لابد وان نلاحظ شىء هام جداً وهو ان جميع هذه الحدود تقبل القسمة على 5
(فيما عدا الحد الأخير) الآن  : a = {1,2,3,4}     l

(عوض فقط فى الحد الأخير)  l      1^4 = 1  وبناء عليه عد التعويض فى n^4 - 1
يزول هذا الواحد تماماً وتقبل القسمة على 5 .

بوضع a = 2   تجد ان "   l         2^4 = 16  والتى اذا طرحنا منها 1 تقبل القسمة على 5

ضع a = 3     اذاً             l       3^4 = 81  والتى اذا طرحنا منها 1 تقبل القسمة على 5

ضع a = 4    اذاً              l     4^4 = 256  والتى اذا طرحنا منها 1 تقبل القسمة على 5

اذاً العبارة E  تقبل القسمة على 10 .

تابع القراءة

0 برهن ان القواسم المشتركة بين a,b هى مجموعة قواسم gsd(a,b) = d

ليكن لدينا عددين a , b  وكان 'a مجموعة جميع قواسم العدد a و 'b مجموعة
جميع قواسم العدد b  بحيث ان المجموعة بالتأكيد تحتوى على عنصر اصغر
وهو 1 وعنصر اكبر وهو العدد نفسه .

a' = {1,a1,a2,...,a}                   ll

b' = {1,b1,b2,...,b}                   ll

الحالة الأولى : gsd(a,b) = 1  والمعنى انهما أوليان فيما بينهما
وفى هذه الحالة فإن القاسم المشترك الوحيد هو 1 وقاسم الواحد
هو ذاته (اذاً العبارة صحيحة)

الحالة الثانية : gsd(a,b) = d  حيث d عدد طبيعى ليس 1 او صفراً .

القواسم المشتركة هى ناتج تقاطع المجموعة 'a مع 'b بحيث انها ايضاً
تحتوى على عنصر اصغر {1} وهى جميع العناصر التى تحقق ai = bi
حيث i = 1,2,3,...  ll  

X = {x : ai = bi , i ∈ N}          ll

اذاً : a تقسم على x  و b تقسم على x اذاً ab تقسم على x
وبما ان قواسم اى عدد طبيعى مجموعة منتهية اذاً مجموعة القواسم
المشتركة بينهما مجموعة منتهية ايضاً، وبالتالى فهى تحوى عنصراً اكبر 'x
(القاسم المشترك الأكبر) وبالتالى فإن المجموعة X ما هى الا مجموعة
جميع قواسم (القاسم المشترك الأكبر)

لإيضاح الفكرة اكثر نقول a = m.d  و b = n.d  حيث d هو القاسم المشترك الأكبر
وبالتالى فإن m , n أوليان فيما بينهما او gsd(m,n) = 1  اذاً اى قواسم مشتركة
للعددين a , b  لابد وان تقسم d فقط لأنه كما قلنا ان m , n اوليان فيما بينهما لعدم
وجود قواسم أخرى اكبر من d ، وبالتالى فإن جميع القواسم المشترك بين a , b
هى مجموعة قواسم d .‏

تابع القراءة

0 أوجد عدد طرق الحصول على المجموع 9 عند رمي ثلاثة احجار نرد مختلفه

فى مثل هذه المسائل نعتمد ابتدائاً على الترتيب، ونتذكر ان جميع الحالات الممكنة للحصول
على مجموعات مكونة من ثلاثة عناصر من المجموعة س* = {1 , 2 , 3 , 4 , 5 , 6}
= (6)³ = 216 مجموعة، والحل عبارة عن مجموعة جزئية منها .

لنأخذ جميع المجموعات التى ليس فيها اى عنصر مكرر ، والتى لا تكرر نفسها (ذاتها)
ومجموعها = 6 ق 3 = 20 .    وهى :-

س = { (1 , 2 , 3) , (1 , 2 , 4) , (1 , 2 , 5) , (1 , 2 , 6) , (1 , 3 , 4) , (1 , 3 , 5) ,
         (1 , 3 , 6) , (1 , 4 , 5) , (1 , 4 , 6) , (1 , 5 , 6) , (2 , 3 , 4) , (2 , 3 , 5) ,
         (2 , 3 , 6) , (2 , 4 , 5) , (2 , 4 , 6) , (2 , 5 , 6) , (3 , 4 , 5) , (3 , 4 , 6) ,
         (3 , 5 , 6) , (4 , 5 , 6) }
       
      

بحيث كل مجموعة من هؤلاء مكررة فى بتكرار 3! = 6

ثم نأخذ المجموعة التى يتكرر فيها عنصران (بغض النظر عن الترتيب)

سَ = { {1 , 1 , 2} , {1 , 1 , 3} , {1 , 1 , 4} , {1 , 1 , 5} , {1 , 1 , 6} , {2 , 2 , 1}
, {2 , 2 , 3} , ...,{2 , 2 , 6}, {3 , 3 , 1} ...,{3 , 3 , 6}, {4 , 4 , 1} ,...., {4 , 4 , 6}
, {5 , 5 , 1} ,..., {5 , 5 , 6} , {6 , 6 , 1} ,..., {6 , 6 , 5} }

بحيث كل مجموعة من هؤلاء مكررة بتكرار 3 .

وأخيراً المجموعة التى يكون يها جميع العناصر متشابهة .

سً = { {1 , 1 , 1} , {2 , 2 , 2} , {3 , 3 , 3} , .... , {6 , 6 , 6} }

وبناء على هذا الترتيب ننتقى من المجموعات الثلاث مايلى ...

ح = { {1 , 2 , 6} , {1 , 3 , 5} , {2 , 3 , 4} }

حَ = { {2 , 2 , 5} , {4 , 4 , 1} }

حً = {3 , 3 , 3}

وبناء عليه يكون عدد الطرق للحصول على المجموع 9 = 1 + (2×3) + (3×3!) = 25 طريقة .

تابع القراءة

0 ق(ر ، ر) + ق[(ر+1) ، ر] + ... + ق(ن ، ر) = ق[(ن+1) ، (ر+1)]

تريد ان تثبت أن :

ق(ر ، ر) + ق[(ر+1) ، ر] + ... + ق(ن ، ر) = ق[(ن+1) ، (ر+1)]

لاحظ أن : ق(ن ، ر) = ق[ر+(ن-ر) ، ر]

من أجل ر=1 فإن العلاقة تكون صحيحة

1      2       3               ن
ق +  ق +  ق + ..... +  ق = 1 + 2 + 3 + .... + ن
  1      1      1                1

لاحظ الطرف الايسر عبارة عن متتابعة حسابية ...

      ن(ن+1)
= ــــــــــــــــــــ
          2

لنتحقق من الطرف الأيسر :-

                              (ن+1)!
ق[(ن+1) ، (ر+1)] = ـــــــــــــــــــــــــ  وبوضع ر=1
                            (ر+1)! (ن-ر)!
                         
      (ن+1)!           (ن+1) × ن × (ن-1)!
= ـــــــــــــــــــــــ = ـــــــــــــــــــــــــــــــــــ
   2 × (ن - 1)!          2 × (ن - 1)!

      ن(ن+1)
= ـــــــــــــــــــ  وبهذا تكون العلاقة صحيحة من أجل ر=1
          2

او ممكن تثبتها اسقرائاً على ن (بدلاً من ر) يعنى عدة محاولات من اجل الوصول الى الحل ..

-------------------------------------------------------------------------------------------------------------------

وأخيراً وجدت ضالتى بعد ان فكرت فيها ابتدائاً، وهى قاعدة باسكال لكن
لم اكمل الحل نظراً لو جود (بعض الأخطاء البسيطة) والتى بدورها جعلتنى
اتخلى عن البرهان بالكلية .

حتى احفظ القاعدة (بعد ان تكون قد فهمتها طبعاً) القاعدة تقول :
                                     
                                          ن
التوفيقة + التوفيقة السابقة لها =  ق
                                             ر

طبعاً كما ترى فهى لغة ركيكة جداً، ولكن حتى احفظك اياها لأنى
سأكررها عشرات المرات فى هذا الحل .. القاعدة الأساسية هى :

ن        (ن-1)        (ن-1)
ق  =       ق  +        ق
  ر            ر           (ر-1)

((سأثبتها فى الملحق القادم حتى لا يحدث هنا ارتباك))

الآن (بإستخدام القاعدة السابقة _قاعدة باسكال) نقول :

ق(ن+1 ، ر+1) = ق(ن ، ر+1) + ق(ن ، ر)

(سنكرر الخوارزمية مرات عديدة (ن مرة مثلاً))

= ق(ن-1 ، ر+1) + ق(ن-1 ، ر) + ق(ن ، ر)

= ق(ن-2 ، ر+1)+ق(ن-2 ، ر) +ق(ن-1 ، ر) + ق(ن ، ر)

= ق(ن-3 ، ر+1)+ق(ن-3 ، ر)+ق(ن-2 ، ر) +ق(ن-1 ، ر) + ق(ن ، ر)
.
.
.
= ق(ر،ر)+ق(ر+1 ، ر) + ق(ر+2 ، ر) + .... + ق(ن ، ر)


توضيح الفقرة السابقة ....

نظل نعيد تكرار الخوارزمية على (او توفيقة فقط) ونترك الباقى كما هو ..
فنلاحظ ان جميعهم تحت الراء (تحت اختيار راء) ولهذا فإن ن تظل مستمرة
فى الصغر الى ان تصل الى توقف معقول وهو راء، وهذا لأنه لا يجوز ان
يكون الحد الأعلى فى التوافيق أكبر من الحد الأسفل .
-------------------------------------------------------------------------------------------------------------

وهذا الإثبات (البسط جداً) لقاعدة باسكال (وضعته فقط من أجل التوضيح)


(ن-1)    (ن-1)         (ن-1)!                 (ن-1)!
    ق +      ق = ــــــــــــــــــــ + ــــــــــــــــــــــــــ
      ر        ر-1     ر! (ن-ر-1)!         (ر-1)! × (ن-ر)!

متى يجوز جمع الكسور ؟ (عند توحيد المقامات) ولهذا يجب توحيد
المقامات بأى شكل .. وهنا اقترح عليك الآتى ...

1) نضرب الكسر الثانى بسطاً ومقاماً فى ر
2) نضرب الكسر الثانى بسطاً ومقاماً فى (ن-ر)

       (ن-ر) (ن-1)!                   ر (ن-1)!
= ـــــــــــــــــــــــــــــــــــــ + ــــــــــــــــــــــــــــــ
    ر! × (ن-ر) (ن-ر-1)!           ر(ر-1)! (ن-ر)!


       (ن-ر) (ن-1)!                  ر  (ن-1)!
= ـــــــــــــــــــــــــــــــــــــ + ــــــــــــــــــــــــــــــ
    ر! × (ن-ر) !                     ر! × (ن-ر)!
 

      (ن-ر) (ن-1)! + ر(ن-1)!          (ن-1)! [(ن-ر + ر)]
= ـــــــــــــــــــــــــــــــــــــــــ = ــــــــــــــــــــــــــــــــــــــ
            ر! (ن-ر)!                          ر! (ن-ر)!


       ن(ن-1)!               ن!
= ــــــــــــــــــــــــ = ـــــــــــــــــ = ق(ن،ر)
      ر! (ن-ر)!           ر! (ن-ر)!


     ن       ن-1   ن-1
اذاً :  ق  =   ق +   ق
        ر        ر      ر-1

والتى تم استعمالها فى حل سؤالك (بشكل متكرر) على الطرف الأيسر . 

-----------------------------------------------------------------------------------------------

بإختصار هذا القانون ينبهك الى انه يمكنك نشر اى توفيقة ق(ن+1 ، ر+1) بعدد
توفيقات = ن-ر+1 ذات فضائات مختلفة تبدأ من ر وتنتهى عند ن وكلها تحت اختيار ر .

لاحظ : من المهم جداً انت تعرف أن آخر حد يمكن الوصول اليه هو ر+1 ق ر+1
والذى يساوى فى الاساس ر ق ر  او ق(ر ، ر)   .. خذ مثال  ...

ق(9+1 ، 3+1) = ق(10 ، 4) = 210

ق(10 ، 4) = ق(9 ، 4) + (9 ، 3)

= ق(8 ، 4) + ق(8 ، 3) + (9 ، 3)

= ق(7 ، 4) + ق(7 ، 3) + ق(8 ، 3) + (9 ، 3)

= ق(6 ، 4) + (6 ، 3) + ق(7 ، 3) + ق(8 ، 3) + (9 ، 3)

= ق(5 ، 4) + ق(5 ، 3) + (6 ، 3) + ق(7 ، 3) + ق(8 ، 3) + (9 ، 3)

= ق(4 ، 4) + (4 ، 3) + ق(5 ، 3) + (6 ، 3) + ق(7 ، 3) + ق(8 ، 3) + (9 ، 3)

كما تلاحظ فإن 4 هنا هى بمثابة ر+1

ق(ر+1 ، ر+1) = ق(ر ، ر) وتم وضعها هكذا تماشياً مع بقية التوافيق التالية لها ..

عدد التوفيقات = 10 - 6 + 1 = 7

مثال آخر : قم بنشر (15 ق 5)


ق(15 ، 5) = ق(4 ، 4)+ق(5، 4)+ق(6 ، 4)+ق(7 ، 4) + .... +ق(14 ، 4)

تابع القراءة

0 اثبت ان ق(ن،1)+ق(ن،3)+ق(ن،5)+.... = 2^(ن-1)

بإختصار تقصد التوافيق الفردية لعدد طبيعى .
                                                   
                                                     ن    ن
نبدأ من نظرية ذات الحدين : (س+أ)^ن = سيجما  ق أ^ر س^(ن-ر)
                                                    ر=0      ر

بوضع س= 1  ، أ = -1  تحصل على المطلوب

                  ن    ن        
(1 - 1)^ن = سيجما  ق (-1)^ر
                 ر=0      ر

     ن      ن      ن     ن
اذاً :   ق -   ق  +  ق -  ق + ..... = 0
        0      1       2     3

انقل التوافيق ذات العوامل السالبة فى طرف تجد ان .

ن       ن      ن             ن      ن      ن
ق  +  ق +  ق + .... =  ق +  ق +  ق + ...
 0       2      4               1      3      5

بمعنى :

عدد التوافيق الفردية = عدد التوافيق الزوجية

ولكن : عدد التوافيق الزوجية + عدد التوافيق الفردية = 2^ن

نفرض أن عدد التوافيق الزوجية = عدد التوافيق الفردية = ع

اذاً : ع + ع = 2^ن  ومنها 2ع = 2^ن  بقسمة الطرفين 2

            2^ن
اذاً ع = ـــــــــــــــ = 2^(ن-1)
             2


اى أن :

ق(ن،1)+ق(ن،3)+ق(ن،5)+.... = 2^(ن-1)

تابع القراءة

0 سؤال فى متسلسلة تايلور

اوجد متسلسلة ماكلورين

1-

y= ln(3+x) ll
put : 2+x = u
ln(3+x) = ln(1+u)ll

u-u^2/2!-u^3/3+....... ll
u is bigger than -1
u is smaler than1

x+2  -( x+2)^2 / 2! + (x+2)^3/3!+.....ll

x is bigger than -1
x is smaler than1


هل هذا الحل صحيح ؟؟ لكن ان كان صحيح الحل الموجود امامى هو

ln(3+x)= ln3  + ln(1+(x/3)) ll
=
ln3 + (x/3)- (x/3)^2/2!+....ll

x is bigger than -3
xis smaler than 3


!!! فكيف الحلان صحيحان ؟؟؟ على الاقل فى المجال الذي يمكن تعويض x فية ؟؟

لاحظ ان
ln(1+x)=x-x^2/2!+x^3/3-......

حل واحد صحيح، وحل 2 قد يكون ايضاً صحيح (لكنى لم اراجعه) فليس من
الضرورى ان يكون نفس الشكل للمتسلسلة ..

حل 1 متأكد منه لكنك لا تكتب رمز المضروب فقط

لاحظ :  ln(x+1) = x - x²/2 + x³/3 - x^4/4 + ... ll

هنا يمكنك تبديل x بـ x+2 للطرفين ..

ln(x+3) = (x+2) - (x+2)²/2 + (x+2)³/3 -  ..... ll

ما الذى صنعه ؟ كل الذى صنعه هو انه وضع x+2 = u

ln(u+1) = u - u²/2 + u³/3 - u^4/4 + ... ll

نعود الى المجال المعرف للمتسلة الأولى :

ln(x+1) = x - x²/2 + x³/3 - x^4/4 + ... ll

مجال التعريف [1 , -1[

لكى تتعرف لماذا قم بنشر دالة اللوغاريتم الطبيعى ..

بحيث أن x اكبر من الصفر (وهذا شىء معروف فى اللوغاريتمات)

f(x) = lnx  ,  f'(x) = 1/x  , f"(x) = -1/x²  , f"'(x) = 2/x³

يبتين لنا من خلال ذلك انه لا يمكن انن نشر هذه الدالة عند الصفر ولكن
يمكن نشر الدالة حول x = 1   ولاحظ ..

f(1) = 0   ,  f'(1) = 1  , f"(1) = -1  , f"'(1) = 2

بصفة عامة المشتقة التى رتبتها عدد زوجى سالبة والتى رتبتها عدد فردى موجبة .

مثلاً المشتقة الرابعة هى -3  والمشتقة الخامسة هى 4 ....وهكذا

بإستعمال متسلسلة تايلور :

f(x) = f(1) + f'(1) (x - 1) + f"(1)/2! (x-1)² + f"'(1)/3! (x - 1)³ +  ...  ll

ln(x) = (x-1) - (x-1)²/2 + (x-1)³/3 - ....ll

نبدل x بـ x+1  للطرفين ...

ln(x+1) = x - x²/2 + x³/3 - x^4/4 + ... ll

الآن لا يمكن ان تكون x=-1 لأنها تجعل x+1=0 وهذا مرفوض

اذاً : المتسلسلة صحيحة من أجل x اكبر من -1

ولكن تم اثبات ان حدود المتسلسلة السابقة متقاربة من أجل x تنتمى للفترة  [1 , -1[

اما المنشور الثانى : فهو اعتقد ابتدائاً ان الدالة هى : f(x) = ln(x+3)  ll

f'(x) = 1/(x+3)   ,  f"(x) = -1/(x+3)²   , f"'(x) = 2/(x+3)³

وهكذا .. الآن قم بنشر الدالة حول x=0

f(0) = ln3  ,  f'(0) = 1/3  ,  f"(0) = -1/9  , f"'(0) = 2/27


ln(x+3) = ln3  + (x/3) - (x²/2*9) + (x³/3*27) - ....   ll

لاحظ يجب ان يكون x + 3  اكبر من الصفر  ومنها x اكبر من -3

ولكن تم اثبات ان حدود المتسلسلة تكون متباعدة عندما x اكبر من 3

ويمكن اثبات التقارب والتباعد بالطريقة الآتية :

                                    س²       س³       س^4
لط(س+1) = د(س) = س - ــــــــــ + ـــــــــــ - ــــــــــــ  + ...
                                     2           3           4


                             س^ن
فنجد أن الحد العام هو : ـــــــــــ  وبوضع س = أ  حيث أ فى الفترة [1 ، -1[
                                ن

             أ^ن
نهــــــــا ـــــــــــــ = 0
ن←∞      ن

عدا ذلك فإن النهاية السابقة = ∞

مثال (للتوضيح فقط) لك ان تتخيل اذا كانت س = 2

                           2^5
ولتكن ن = 5  فإن : ــــــــــــــــ = 6.4
                             5

وهكذا ترى ان تقدم البسط (فى هذه الحالة) نحو اللانهاية اسرع بكثير من المقام
ولذا فإن النهاية السابقة = ∞  من أجل س أكبر من الواحد . 

تابع القراءة

7 اثبت ان عدد المجموعات الجزئية لأى مجموعة عدد عناصرها ن هو 2^ن

اعتقد ان هذا شىء أساسى فى المجموعات .

عدد جميع المجموعات الجزئية لأى مجموعة عدد عناصرها ن هو 2^ن

مثال : لتكن المجموعة س = {1 ، 2 ، 3}

ولتكن ج = اتحاد جميع مجموعات س الجزئية .

ج = {

{} , {1} , {2} , {3} , {1 ، 2} , {1 ، 3} , {2 ، 3} , {1 ، 2 ، 3}

}

حيث {} تعنى المجموعة الخالية .

بالإستقراء الرياضى : لتكن س هى المجموعة الخالية اذاً هى تحتوى
على عنصر واحد وعدد عناصراً صفر، ولذلك فإن  2^0 = 1 وهذا يعنى
ان العلاقة صحيحة، كذا ايضاً اذا كان عدد عناصر المجموعة عنصر واحد
فقط فإن عدد المجموعات الجزئية = 2^1 = 2 وهذا صحيح .

وفى الحقيقة قد جربت الإثبات بنفسى سابقاً (اى انى لم اتقيد بإثبات معين)

وكان كالتالى ...

ليكن عدد عناصر المجموعة هو ن فإنه المجموعة الخالية تنتمى لأى
مجموعة، وبذلك نستطيع ان نرمز لها بالرمز (صفر ، ليس كعدد وانما كرمز)

0  ====> ن ق 0

1 ====> ن ق 1

ما معنى ن ق 1  ؟

ن ق 1 = ن  = عدد جميع المجموعات الجزئية التى تتألف من عنصر واحد ..
وهكذا فإنك اذا ما تابعت الحلقة بإستمرار تجد اننا نتحدث عن عوامل ذات الحدين .

0  ====> ن ق 0

1 ====> ن ق 1

2 ====> ن ق 2

3 ====> ن ق 3
.
.
.
ن ====> ن ق ن

اذاً : (ن ق 0) + (ن ق 1) + (ن ق 2) + .... + (ن ق ن) = 2^ن

والإثبات من نظرية ذات الحدين نفسها ...

                                       ن     ن
النظرية هى : (س + أ)^ن = سيجما   ق أ^ر س^(ن-ر)
                                     ر=0        ر

بوضع س = أ = 1  للطرفين ...

                    ن     ن
(1 + 1)^ن = سيجما  ق 1^ر × 1^(ن-ر)
                   ر=0      ر

         ن    ن
اذاً : سيجما   ق  = 2^ن       وهو المطلوب اثباته .
       ر=0       ر

اذاً : عدد المجموعات الجزئية لأى مجموعة منتهية عدد عناصرها ن هو 2^ن .

ولكى نثبت ما سبق بالإستقراء الرياضى يجب ان نتعرف على مفهوم هام جداً وهو
اذا كان لدينا مجموعتين س ، ص وكان عدد عناصر س هو ن وعدد عناصر ص هو م
فإن عدد جميع المجموعات التى تتكون من عنصرين فقط من المجموعتين س ، ص
تتلخص فى القانون س × ص = ن × م


فإذا قولنا أن المجموعة س = {أ ، ب ، جـ}  وكانت عندنا مجموعة اخرى

ص = {ع ، غ}

فإن : س × ص = { {أ ، ع} , {أ ، غ} , {ب ، ع} , {ب ، غ} , {جـ ، ع} , {جـ ، غ}

}

وهم عبارة عن 6 عناصر كل عنصر عبارة عن مجموعة مكون من عنصرين ...
نظراً لأن كل عنصر من عناصر المجموعة س يقابله عنصرين من المجموعة ص .
او العكس يمكن ان نقول كل عنصر من عناصر المجموعة ص يقابلة ثلاث عناصر
من المجموعة س ... وهذا كافى لتكوين جميع المجموعات المكونة من عنصرين ...

فإذا عودنا الى مثال حى مما ذكرناه سابقاً :-

ليكن

ج = {

{} , {1} , {2} , {3} , {1 ، 2} , {1 ، 3} , {2 ، 3} , {1 ، 2 ، 3}

}

ج َ = { {} , {4} }

ج × جَ = {

{} , {1} , {2} , {3} , {1 ، 2} , {1 ، 3} , {2 ، 3} , {1 ، 2 ، 3} ,
{4} , {1 ، 4} , {2 ، 4} , {3 ، 4} , {1 ، 2 ، 4} , {1 ، 3 ، 4} , {2 ، 3 ، 4} ,
{1 ، 2 ، 3 ، 4}

}

اذاً مفهوم عدد عناصر المجموعة التالية هو 2× عدد عناصر المجموعة الجزئية السابقة لها

وبناء على هذه المفاهيم الأساسية : نقول العلاقة 2^ن من أجل ن = 0 ، ن = 1 صحيحة ايضاً
ويمكن تجربتها بأكثر من ذلك ان شئت، ثم نفرض صحتها عندما ن=ك  ، والآن عدد عناصر المجموعة
الجزئية التى تليها تتحد بالآتى ..

لتكن عدد المجموعات الجزئية للمجموعة س هو 2^ك  حيث ك عدد طبيعى .
الآن لإيجاد المجموعة التى تليها ما علينا سوى ضربها فى مجموعة ص تتكون
من عنصر وحيد أ  فتكون مجموعاتها الجزئية { {} , {أ} }

عدد المجموعات الجزئية للمجموعة س = 2^ك
وعدد العناصر الجزئية للمجموعة ص = 2

اذاً عدد عناصر المجموعة الجديدة = س×ص = 2 × 2^ك = 2^(ك+1)

اذاً العلاقة صحيحة ...

تابع القراءة

7 أوجد الحد التالى للمتابعة 1 ، 2 ، 4 ، 7 ، 11 ، .....

من خلال تتبع حالات الحدود الأولى ومقارنتها بسابقيها نلاحظ الآتى :


الحد الأول = 1                (فرضاً كحد ابتدائى)

الحد الثانى = 1 + 1

الحد الثالث = 2 + 2

الحد الرابع = 4 + 3

الحد الخامس = 7 + 4

الحد السادس = 11 + 5 = 16

بإختصار : الحد = قيمة الحد السابق له + رتبته

او نقول الحد العام هو : ح(ن) = ح(ن-1) + (ن-1)

المتتابعة هى : 1 ، 2 ، 4 ، 7 ، 11 ، 16 ، ...

الى هنا سؤالك انتهى، ولكن ماذا لو كنا نرغب فى ايجاد الحد المائة مثلاً؟
هل تنظل نتبع جميع الحدود الى ان نصل الى الحد الذى رتبته 99 ؟
بالطبع هذا شىء ممل ومتعب، لذلك اقترح عليك اتباع الطريقة الآتية .

ح(1) = 1           (شرط بدئى)

بما أن : الحد = الحد السابق له + رتبته     اذاً

ح(ن) = ح(ن-1) + (ن-1)

= ح(ن-2)+(ن-2)+(ن-1)

= ح(ن-3)+(ن-3)+(ن-2)+(ن-1)

= ح(ن-4)+(ن-4)+(ن-3)+(ن-2)+(ن-1)
.
.
.
= ح(1) + 1 + 2 + 3 + ...... + (ن-4)+(ن-3)+(ن-2)+(ن-1)

= 1 + 1 + 2 + 3 + ........ + (ن-1)

نلاحظ انها = 1 + مجموع متتابعة حسابية حدها الأول 1 واساسها 1
وحدها الأخير (ن-1) .

         ن (ن-1)      
= 1 + ــــــــــــــــ
             2
                        ن(ن-1)
اذاً : ح(ن) = 1  + ــــــــــــــــ
                            2

                         6 (6 - 1)
مثال : ح(6) = 1 + ــــــــــــــــــــ = 16
                             2

                     100 × 99
ح(100) = 1 + ــــــــــــــــــــــ = 4951
                         2

                       1000 × 999
ح(1000) = 1 + ـــــــــــــــــــــــــــ = 499501
                             2

تابع القراءة

0 ص = س^4 +6س^3+11س^2+6س فإثبت انه من مضاعفات العدد 24 من أجل س عدد طبيعى .

ص = س^4 + 6س³ + 11س² + 6س بأخذ س عامل مشترك ..

ص = س(س³ + 6س² + 11س + 6)

بتعميل حدود المعادلة (بالتقسيم)

ص = س(س³ + 1 + 6س² + 11س + 5)

ص = س[(س+1) (س² - س + 1) + (6س+5) (س+1)]

بأخذ (س+1) عامل مشترك ...

ص = س(س+1) [س² - س + 1 + 6س + 5]

ص = س(س+1) (س² + 5س + 6)

ص = س(س+1) (س+2)(س+3)

ولكن س عدد طبيعى ، والعلاقة س(س+1) (س+2)(س+3)
هى تعبير عن حاصل ضرب اربعة  أعداد طبيعية متتالية، اذاً تقبل
القسمة على مضروب الأربعة 4!  اى انها تقبل القسمة على 24 .

نقول أن : ن ل 4  تقبل القسمة على مضروب الأربعة .

(ان وجدت طريقة أخرى سأضعها)

..........................................................................................................

** وهذه محاولة جادة لإثبات الحصول على الطريقة **

لاحظ العلاقة : س(س+1) (س+2)(س+3)

تعنى حاصل ضرب 4 أعداد طبيعية متتالية .

لنفرض أن العدد الأخير فى هذه الأعداد الأربعة هو ن .

اذاً العلاقة السابقة تكافىء ..

ن(ن - 1)(ن - 2) ( ن - 3) = ن ل 4

او تقرأ ن تباديل 4

                          ن!                ن!
ولكن :  ن ل 4 = ــــــــــــــــــ = ــــــــــــــــــ
                       (ن - 4)!        (ن - 4)!


     ن(ن-1)(ن-2) .... × 4 × 3 × 2 × 1
= ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
                     (ن - 4)!

ولكن أفضل اثباتها بالإستقراء على ن بحيث ن عدد طبيعى أكبر من او يساوى 4

الآن من أجل ن = 4  فإن 4 ل 4 = 4! = 24 الآن نفرض أن العلاقة صحيحة من أجل

                 ك              ك!
ن = ك   اذاً     ل  = ـــــــــــــــــــــ = 4! م
                     4       (ك - 4)!

حيث م عدد طبيعى ما لا نعرفه (ليس شرط الترتيب هنا) ..
والآن نثبت ان العبارة صحيحة من أجل ن = ك+1

اى لابد ان نثبت أن :

(ك+1)             (ك+1)!
      ل  = ـــــــــــــــــــــــــــــــــ
        4         [(ك+1) - 4]!

السؤال كيف نحصل على ك+1 ؟  عن طريقة ضرب الطرفين فى ك+1 ومن
ثم قسمة الطرفين على (ك - 3)   ... اعلم ان هذه الخطوة غير واضحة .

سأعطى مثالاً للتوضيح : اذا قولنا 8 ل 4 = 8 × 7 × 6 × 5
ونريد ان نحصل على 9 ل 4 من خلالها .. ما الذى نفعله ؟
كل ما الأمر انك تضرب 8 ل 4 فى 9 ومن ثم تقسم على 5
فيكون : 9 ل 4 = 9 × 8 × 7 × 6

ليكن 8 هى ك  اذاً  9 هى ك+1

وطالما ان 8 هى ك  اذاً  ك
                              ل = ك(ك-1)(ك-2)(ك-3)
                                4

اى ان الحد الأخير الذى قسمنا عليه هو  (ك - 3)

بعد هذا التوضيح نقول (بضرب الطرفين فى (ك+1) ومن ثم القسمة على (ك-3)


ك
ل × (ك+1)
 4                       (ك+1)  ك!                    (ك+1)
ـــــــــــــــــــــــــ = ـــــــــــــــــــــــــــــ = 4!م×ــــــــــــــــ
   (ك - 3)            (ك-3)   (ك - 4)!               (ك-3)


(ك+1)          (ك+1)!              (ك+1)!                  (ك+1)
      ل  = ــــــــــــــــــــــ = ــــــــــــــــــــــــــ = 4!م×ـــــــــــــــ
        4         (ك-3)!           [(ك+1) - 4]!              (ك-3)


                             (ك+1)
ولكن بالفعل :  4!م × ــــــــــــــــــ من مضاعفات العدد 4! = 24
                             (ك-3)

                        ك+1
ولكن هل فعلاً :م× ــــــــــ عدد طبيعى  من أجل ك = {4 ، 5 ، 6 ، .....}  ؟
                        ك-3

اما م فهو عدد طبيعى ....

هذا هو اساس البرهان، وهذا ما سنعتمد عليه ... اذا وضعت ك=4

م( 4 + 1)                                          م(5 + 1)                          
ــــــــــــــــــ = 5م  واذا وضعت ك = 5  فإن : ـــــــــــــــــ = 3م
   4 - 3                                                5 - 3

وكلاً من 5م ، 3م أعداد طبيعية ... ضع ك = 6  

م(6 + 1)        7م
ــــــــــــــــ = ــــــــــــ  كما تلاحظ هنا فلا نقول ان 7م على 3 عدد غير طبيعى
  6 - 3            3

لأن م عدد طبيعى (يحقق شروط معينة، وليس اى عدد طبيعى)

لذلك دعك من كل ما سبق (أى احد يقرأ هذا الكلام ووصل لنتيجة يكتبها
ولا يبخل علينا ...)

░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░░
واليك عزيزى الطريقة المبسطة التى وعدتك بها وتتلخص فى الآتى

حاصل ضرب اربعة أعداد متتالية يقبل القسمة على 4 (حقيقة)

وهذا لأن بواقى العدد 4 محصورة فى المجموعة {1 ، 2 ، 3}
فإن لم يقبل العدد الأول فالثانى، وان لم يقبل الثانى فالثالث، وان
لم يقبل الثالث فلابد ان يقبل العدد الرابع على 4 .

مثال : 9 × 8 × 7 × 6

تجد أن الأول 9 لا يقبل القسمة على 4
لكن الثانى 8 يقبل القسمة على 4  وهكذا ...

اذاً : لا شك ان حاصل ضرب اربع أعداد طبيعية متتالية يقبل القسمة على 4

الآن : 4! = 24 = 4 × 6  اذاً بقى لنا ان نثبت ان العدد يقبل القسمة على 6

ولكن ما هى الـ 6 ؟   6 = 3 × 2

لنفترض الآن ان حدث وقوع عدد يقبل القسمة على 4 قد وقع بالفعل
(قد يكون الأول - الثانى - الثانى - الرابع) اى ً منهم قد وقع الإختيار
عليه انه يقبل القسمة على 4 يتبقى لدينا ثلاثة أعداد لابد ان احدهم
يقبل القسمة على 3 ، ثم يتبقى لدينا عددين لا بد اون احدهما يقبل
القسمة على 2 .

اذاً العدد يقبل القسمة على 4 × 3 × 2 × 1 = 24 = 4!

ولكى اوضح المسألة أكثر نقول : حاصل ضرب أى أعداد طبيعية متالية عددها ن
تقبل القسمة ن ، ولكنها تقبل القسمة على ن - 1 ايضاً وتقبل القسمة على  ن - 2
و ن - 3  ... وهكذا الى ان ننتهى عند العدد 1 .

مثال : اذا قولنا ان حاصل ضرب ثلاثة أعداد طبيعية متتالية يقبل القسمة على 3 (حقيقة)

اذاً حاصل ضرب اربعة أعداد طبيعية متتالية يقبل القسمة على 3 ايضاً (غير قبول القسمة على 4)

لماذا ؟ لأن حاصل ضرب اربعة أعداد طبيعية متتالية تعنى اننا قد حصلنا بالفعل على ثلاثة
أعداد طبيعية متتالية، وتعنى ايضاً بالفعل اننا قد حصلنا على عددين متتاليين .. والمسألة
اصحبت هكذا أكثر وضوحاً .( وهى تشبه تكرار خوارزمية ما)


الإستنتاج الأخير : حاصل ضرب مجموعة أعداد طبيعية متتالية عدد عناصر ن
تقبل القسمة على ن!  .

.................................................................................................

يوجد اثبات آخر مباشر وهو :

                          ن!              
ولكن :  ن ل 4 = ــــــــــــــــــ  بقسمة الطرفين على 4!
                      (ن - 4)!      

       ن ل 4                 ن!               ن
= ـــــــــــــــــــــ = ـــــــــــــــــــــــــ =    ق
         4!                (ن - 4)! 4!            4

وهذا يتطلب منك ان تثبت ان التوافيق لأعداد طبيعيى تعطى عدد طبيعى دائماً

والمعنى انه عند قسمة ن ل 4  على مضروب 4 اعطتنا ن ق 4 والذى هو عدد
طبيعى اذاً ن ل 4 قبل القسمة على 4! لأن خارج القسمة كان عدد طبيعى وهو
ن ق 4 .

ولكن يبقى من وجهة نظرى البرهان (المبسط) الذى قدمته دليل يثبت
ان التوافيق دائماً عدد طبيعى (التى على الشكل ن ق ر) حيث كلاً من
ن ، ر أعداد الطبيعية ، ن أكبر من او تساوى ر  .

تابع القراءة

0 اوجد مشتقة جا^-1(س) بإستخدام التعريف سَ = (صَ)^-1

ابدأ معك من اى دالة بصفة عامة (لأنى الاحظ ان هذا ما تقصده)

نفرض د : دالة د(س) لها دالة عكسية وهى د^-1(س) اذاً هذا شرط
اساسى ان تكون للدالة نظير الدالة (او الدالة العكسية)

مثال سريع ...

ص = هـ^س   ومنها صَ = هـ^س

س = لوص      ومنها  سَ = 1/ص

ويمكن ايجاد س َ بطريقة أخرى ..... وهذا ما اوردته ..

                           1              1
سَ =  (صَ)^-1 = ـــــــــــــ = ـــــــــــــــ
                       هـ^س          ص

بتطبيق هذه الخطوة على الدوال المثلثية والزائدية بحكم انها قابلة
لأن تكون لها دالة عكسية ..

مثال : د(س) = جاس     او  :  ص = جاس   كتابة أخرى

اذاً  صَ = جتاس  ، والآن ايجاد مشتقة الدالة العكسية يعنى بالأمر

اننا نريد سَ  .

             1                    1
سَ = ـــــــــــــــــ = ــــــــــــــــــــــــ
           (صَ)            (جتاس)

وهنا لابد من تحويل جتاس الى جاس لأن الدالة الأساسية هى جاس .

 
             1                          1
= ـــــــــــــــــــــــــــــ = ـــــــــــــــــــــــ
    جذر(1 - جا²س)         جذر( 1 - ص²)

وطبعاً س ، او ص او ع .. كلها رموز اعتباطية .. يعنى بصفة عامة

اذا كانت الدالة هى : د(س) = جا^-1(س)  فإن

                       1
دَ(س) = ــــــــــــــــــــــــــــ
             جذر( 1 - س²)

وهذه وجهة نظرى فى اثبات الطريقة، بدأت معك بإشتقاق دالة الأس
الطبيعى، لأن اى دالة تستطيع وضعها فى صورة دالة الأس الطبيعى .

مثال : د(س) = 2^س  هى نفسها د(س) = هـ^لط(2^س)

بإختصار كل دالة   ص = هـ^لط(د(س))

الآن نشتق الطرفين بالنسبة لـ ص

      دَ(س)
1 = ـــــــــــــ × هـ^(لط(د(س)) × سَ
     د(س)

ولكن د(س) = هـ^(لط(د(س)) = ص  بالتعويض ...

      دَ(س)
1 = ـــــــــــــ × ص × سَ
       ص
                                                  1
اذاً : دَ(س) × سَ = 1   ومنها  سَ =  ـــــــــــ
                                              دَ(س)

او بإختصار نقول : سَ = (صَ)^-1

.....................................................................................................
مثال على مشتقة  ص = جازس  (اى الجيب الزائدى)

ويمكن كتابتها بالطريقة : ص = هـ^لط(جازس)

الآن اشتق الطرفين بالنسبة لـ ص .

         (جازس) َ
1 = ـــــــــــــــــــــ × هـ^لط(جازس) × سَ
         جازس

ولكن جازس =  هـ^لط(جازس) = ص  

                                                     1
اذاً : 1 = (جازس) َ × سَ  ومنها سَ = ــــــــــــــــــ
                                                (جازس)َ

              1                  
سَ = ـــــــــــــــــ   ولكن جتاز²س - جاز²س = 1
         جتازس

ومنها  جتازس = جذر(1 + جاز²س)

                         1                          1
اذاً : سَ = ــــــــــــــــــــــــــــــ = ــــــــــــــــــــــــــــــ
              جذر(1 + جاز²س)         جذر(1 + ص²)


والتى كان يمكن حلها مباشرة ً من عند الخطوة سَ = (صَ)^-1

             1                 1                         1
سَ = ــــــــــــــــ = ـــــــــــــــــــــــــ = ـــــــــــــــــــــــــــ
         جتازس     جذر(1 + جاز²س)      جذر(1 + ص²)

..................................................................................

مثال 3) على دالة ليس لها معكوس .

ص = س²

ويمكنك معرفة ذلك هندسياً وجبرياً .. اما هندسياً فأسهل شىء
هو الإختبار الخط الأفقى (كما هو موضح بالرسم) فتجده تقطع
الدالة فى نقتطين، اذاً الدالة العكسية غير موجودة .

او جبرياً مباشرة ً س = جذر(ص)  او س = - جذر(ص)

نقول : ص =  هـ^لط(س²)  اشتق الطرفين بالنسبة لـ ص

        2س
1 = ــــــــــــــ ×  هـ^لط(س²) × سَ
        س²

                                    1                                
1 = 2س سَ  ومنها سَ = ـــــــــــــ
                                 2س

ولكن س = جذر(ص) او س = - جذر(ص)

وهذا يعنى ان الدالة العكسية غير موجودة . 

تابع القراءة

0 حل لغز السيارة

ثلاثة طلبة رياضيات يتجولون في مدينة ، فجأة لاحظوا سائق سيارة ارتكب مخالفة خطيرة في الطريق ، وفر السائق مسرعا . لم يتذكر أي منهم رقم السيارة المكون من أربعة أرقام ولكن تذكر أحدهم أن الرقمين الأولين متشابهين ، ثم قال الآخر وأنا أتذكر أيضا أن الرقمين الأخيرين متشابهين ، وقال الثالث وأنا أتذكر أن رقم السيارة مربع تــام . هل يمكن باستعمال هذه الخاصيات الثلاث معرفة رقم السيارة ؟؟؟؟

حسب فهمى لمعطيات المسألة اقول :

نفرض أن س ، س ، ص ، ص هى ارقام الآحاد والعشرات والمئات والأولوف
على الترتيب .

الآن نضع العدد المشار اليه فى صورة النظام العشرى ..

س + 10س + 100ص + 1000ص = ن²

= 11س + 1100ص = ن²

حيث ن عدد طبيعى فى الفترة ينتمى لـ [32 ، (10)²[

لماذا ؟ لأن اصغر مربع كامل مكون من اربع ارقام هو 1024
والذى يساوى (32)² واكبر مربع هو ما قبل الـ 10000 مباشرة ً

كلاً من س ، ص ينتميان الى المجموعة {1 ، 2 ، 3 ، .... ،9}

وهو جميع الإحتمالات التى نرقم بها الخانات العشرية ...

س = {1 ، 2 ، 3 ، ........ ،9}

ص = {1 ، 2 ، 3 ، ........ ،9}


وجميع الإحتمالات الممكنة هى (نرمز لها بالمجموعة ع)

ع = {

       {1 , 2} , {1 , 3} , {1 , 4} , ..... ,{1 , 9}
       {2 , 1} , {1 , 3} , {1 , 4} , ..... ,{1 , 9}
       {3 , 1} , {3 , 2} , {3 , 4} , ..... ,{1 , 9}
       .
       .
       .
      {9 , 1} , {9 , 2} , {9 , 3} , ..... , {9 , 8}

}

مثلاً المجموعة  {1 , 2} = المجموعة   {2 , 1} لذلك سمع لك بتجربة الإثنين ..


11(1) + 1100(2) = 2211  ليس مربع كامل ...

اعكس وضع الأرقام .. 1122 ايضاً ليست مربع كامل ...

اذاً انت بحاجة لتجربة 72 امكانية ... ولكن هذا شىء صعب لذلك ارجع
الى المعادلة الأساسية وهى :

11س + 1100ص = ن²  ومنها 11س = ن² - 1100ص

          ن²
س = ــــــــــ - 100ص
         11

من أجل س عدد طبيعى  ===> اذاً ينبغى ان يقبل ن² القسمة على 11

                                            ن²
الشرط الثانى يجب أن يتحقق أن : ــــــــــ  -  100ص
                                            11

هو ناتج محصور فى المجموعة {1 ، 2 ، 3 ، ...... ، 9}

بما ان ن² من مضاعفات العدد 11 اذاً ينبغى ان تكون ن من مضاعفات العدد 11

نفرض أن : ن = 11م  حيث م عدد طبيعى           ...   اذاً


ولكن كما قولنا ن محصورة فى المجموعة من 32  الى 100
هذا يعنى ان : 11م محصورة فى المجموعة من 32 الى 100
من اجل م عدد طبيعى .. اذاً ينبغى ان نأخذ جميع العناصر
التى من مضاعفات العدد 11 والمحصورة من 32 الى 100
وجميعها هى :

33 ، 44 ، 55 ، 66 ، 77 ، 88 ، 99  بالتعويض بكل واحدة فى العلاقة


          ن²
س = ــــــــــ - 100ص   من اجل  ن = 33   فإن
         11

        (33)²
س = ــــــــــ - 100ص    ولكن الشرط الثانى يجب ان يتحقق
         11

لذلك فإن وضع ص = 1 هنا يجعل س = -1 ، وبناء عليه فإن وضع قيمة
لـ ص اكبر من الواحد يجعلها سالبة ايضاً ...

الخطوة الثانية : من اجل ن = 44


        (44)²
س = ــــــــــ - 100ص = 176 - 100ص
         11

من اجل ص = 1  فإن : س = 176 - 100 = 76  وهذا مرفوض لأن س محصورة
فى المجموعة من 1 الى 9  واذا وضعت ص = 2 فإن س تكون سالبة ..

الخطوة الثالثة : من أجل ن = 55

        (55)²
س = ــــــــــ - 100ص = 275 - 100ص
         11

لا يتحقق شىء ..

الخطوة الرابعة : من اجل ن = 66

         (66)²
س = ــــــــــ - 100ص = 396 - 100ص
          11

من اجل ص = 4 فإن : س = -4  وهذا مرفوض ..

الخطوة الخامسة : من اجل ن = 77

        (77)²
س = ــــــــــ - 100ص = 539 - 100ص
         11

ايضاً لن يتحقق شىء ...

الخطوة السادسة : من اجل ن = 88

         (88)²
س = ــــــــــ - 100ص = 704 - 100ص
         11

من أجل ص = 7  فإن  س = 704 - 700 = 4

ويكون العدد هو : 7744 وهو مربع كامل جذره = 88

الخطوة السابعة ( والأخيرة) : من اجل  ن = 99

        (99)²
س = ــــــــــ - 100ص = 891 - 100ص
         11

من أجل ص = 9  فإن س تكون سالبة وهذا مرفوض ..

اذاً العدد الوحيد هو : 7744

تابع القراءة